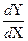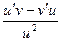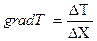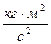grad что такое в математике
Градиент функции что это
Определение. Вектор с координатами 
называется градиентом функции u=f(x,y,z) и обозначается
С помощью оператора Гамильтона ( или набла-оператора)
можно кратко записать градиент функции:
Градиент функции в данной точке указывает направление наиболее быстрого возрастания функции.
Модуль градиента 
определяет крутизну наибольшего ската или подъема поверхности u=f(x,y,z).
Как найти градиент
Решение. Для функции двух переменных градиент находим по формуле
2) Подставляем в формулу, получаем градиент функции в произвольной точке
Найти градиент функции можно также с помощью калькулятора
3) Подставляем координаты точки M(-5;7), получаем
4) Находим модуль градиента в точке M(-5;7) по формуле:
Вывод: Если движение происходит в направлении градиента функции (50;-140), то получаем скорость максимального изменения функции 148,66 в точке M(-5;7).
Производная по направлению
Если движение будет происходить в других направлениях, то скорость будет меньше. Покажем это на примере.
Решение. Пункты 1),2) и 3) совпадают с решением примера 1.
СОДЕРЖАНИЕ
Мотивация
Обозначение
Определение
Когда функция также зависит от параметра, такого как время, градиент часто относится просто к вектору только его пространственных производных (см. Пространственный градиент ).
Декартовы координаты
В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, задается следующим образом:
Цилиндрические и сферические координаты
В цилиндрических координатах с евклидовой метрикой градиент задается следующим образом:
В сферических координатах градиент определяется как:
Общие координаты
Последнее выражение соответствует приведенным выше выражениям для цилиндрических и сферических координат.
Связь с производной
Связь с полной производной
С вычислительной точки зрения, учитывая касательный вектор, вектор можно умножить на производную (в виде матриц), что равносильно взятию скалярного произведения с градиентом:
( d ж п ) ( v ) знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋯ ∂ ж ∂ Икс п ( п ) ] [ v 1 ⋮ v п ] знак равно ∑ я знак равно 1 п ∂ ж ∂ Икс я ( п ) v я знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋮ ∂ ж ∂ Икс п ( п ) ] ⋅ [ v 1 ⋮ v п ] знак равно ∇ ж ( п ) ⋅ v <\ Displaystyle (df_
) (v) = <\ begin 
Дифференциальная или (внешняя) производная
Наилучшее линейное приближение дифференцируемой функции
Градиент связан с дифференциалом формулой
Если R n рассматривается как пространство векторов-столбцов (размерности n ) (действительных чисел), то можно рассматривать df как вектор-строку с компонентами
Линейное приближение к функции
Связь с производной Фреше
Как следствие, обычные свойства производной сохраняются для градиента, хотя градиент сам по себе не является производной, а скорее двойственен производной:
Другие свойства и применения
Наборы уровней
В более общем смысле, любая вложенная гиперповерхность в римановом многообразии может быть вырезана уравнением вида F ( P ) = 0 таким, что dF нигде не равно нулю. Тогда градиент F нормален к гиперповерхности.
Консервативные векторные поля и градиентная теорема
Градиент функции называется градиентным полем. (Непрерывное) поле градиента всегда является консервативным векторным полем : его линейный интеграл вдоль любого пути зависит только от конечных точек пути и может быть вычислен с помощью градиентной теоремы (основная теорема исчисления для линейных интегралов). И наоборот, (непрерывное) консервативное векторное поле всегда является градиентом функции.
Обобщения
Якобиан
Градиент векторного поля
Поскольку полная производная векторного поля является линейным отображением векторов в векторы, это тензорная величина.
(где используется обозначение суммирования Эйнштейна, а тензорное произведение векторов e i и e k является диадическим тензором типа (2,0)). В целом это выражение равно транспонированной матрице Якоби:
В криволинейных координатах или, в более общем смысле, на изогнутом многообразии градиент включает символы Кристоффеля :
Выражаясь более инвариантно, градиент векторного поля f может быть определен связностью Леви-Чивиты и метрическим тензором:
Римановы многообразия
где X j обозначает j- й компонент X в этой координатной карте.
Итак, локальная форма градиента принимает вид:
Производная по направлению, градиент функции: объяснение, примеры
Понятие производной по направлению
Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.
Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:
Величину отрезка MM 1 можно обозначить 
.
Функция u = f(M) при этом получит приращение
.
Определение производной по направлению. Предел отношения 
при 
, если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается 
, то есть
.
Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:
.
Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.
Примеры нахождения производной по направлению
Пример 1. Найти производную функции 
в точке M 0 (1; 2; 3) по направлению вектора 
.
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
Теперь можем найти производную по направлению данной функции по её формуле:
Пример 3. Найти производную функции 
в точке M 0 (1; 1; 1) по направлению вектора 
.
Решение. Найдём направляющие косинусы вектора
Найдём частные производные функции в точке M 0 :
Следовательно, можем найти производную по направлению данной функции по её формуле:
.
Градиент функции
Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат являются значения частных производных 
, 
, 
этой функции в соответствующей точке:
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.
Для градиента функции двух переменных формула короче:
.
Решение. Найдём частные производные функции в точке M 0 :
Следовательно, можем записать искомый градиент данной функции:
.
Значение слова «градиент»
[От лат. gradiens, gradientis — шагающий]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Например, если взять в качестве
высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
С математической точки зрения на градиент можно смотреть как на:
1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента
2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных
3. Строки Матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).
Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.
Градиент функции
Рисунок 3.
Приращение функции – изменение функции.
у 
А В 
 |
Производной функциейназывается предел отношения приращения функции к приращению аргумента при последнем, стремящемся к нулю.
y’= lim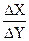 
= 
Процесс вычисления производной называется дифференцированием.
Дифференциалом функции → y = f(x) называется dy = y’dx, где dx – произвольное приращение аргумента.
y’=
Интегрирование – процесс обратный дифференцированию.
Основные свойства производной:
(
)’=
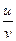
Градиентом физической величины называется отношение приращения этой функции к расстоянию, на котором это приращение происходит. Градиент физической величины – величина векторная и направлена в сторону увеличения значений этой величины.
 |
● ●
Физической величиной называют все то, что можно измерить количественно. Физические величины бывают векторные и скалярные.
Векторные величины, кроме численного значения, имеют еще и направление. Скалярные величины имеют только численные значения.
Для получения числовых значений физических величин необходимо измерять эти физические величины. Измерение физической величины сводится к сравнению её с однородной физической величиной, принятой за единицу. Для каждой физической величины эту единицу можно выбирать произвольно. Однако на практике для удобства выбраны единицы только для семи физических величин, называемых основными. Единицы всех остальных физических величин устанавливают на основании законов, связывающих эти величины с основными. Совокупность всех единиц измерения физических величин называется системой единиц.
Международная система единиц «СИ»
7. Количество вещества моль
1. Плоский угол рад
2. Телесный угол срад
Все остальные являются производными.
[H] =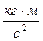 
; [Дж] = 
Измерить физическую величину, значит сравнить ее с единицей измерения (эталоном).