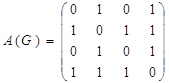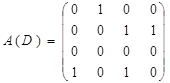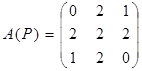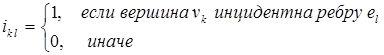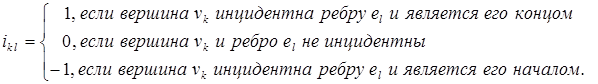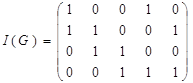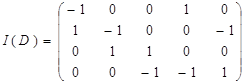Лемма о рукопожатиях что такое

Лемма о рукопожатиях

Лемма является следствием формулы суммы степеней, также иногда называемой леммой о рукопожатиях.

для графа с множеством вершин V и множеством рёбер E. Оба результата доказаны Эйлером в его знаменитом докладе о семи мостах Кёнигсберга (1736). Эта работа положила начало исследованиям в области теории графов.

Вершины нечётных степеней графа иногда называются нечётными узлами или нечётными вершинами. Используя эту терминологию, можно перефразировать лемму таким образом: каждый граф имеет чётное число нечётных вершин.

Связанные понятия

В теории графов циркулянтным графом называется неориентированный граф, имеющий циклическую группу симметрий, которая включает симметрию, переводящую любую вершину в любую другую вершину.

В теории графов рёберным графом L(G) неориентированного графа G называется граф L(G), представляющий соседство рёбер графа G.

В теории графов короной с 2n вершинами называется неориентированный граф с двумя наборами вершин ui и vi и рёбрами между ui и vj, если i ≠ j. Можно рассматривать корону как полный двудольный граф, из которого удалено совершенное паросочетание, как двойное покрытие двудольным графом полного графа, или как двудольный граф Кнезера Hn,1, представляющий подмножества из 1 элемента и (n − 1) элементов множества из n элементов с рёбрами между двумя подмножествами, если одно подмножество содержится в другом.

В теории графов порождённым путём в неориентированном графе G называется путь, являющийся порождённым подграфом G. Таким образом, это последовательность вершин в G такая, что любые две смежные вершины в последовательности соединены ребром в G, и любые две несмежные вершины последовательности не соединены ребром G. Порождённый путь иногда называют змеёй и задача поиска самого длинного порождённого пути в графах гиперкубов известна как задача о змее в коробке.

Орграф называется сильно связным (англ. strongly connected), если любые две его вершины сильно связны. Две вершины s и t любого графа сильно связны, если существует ориентированный путь из s в t и ориентированный путь из t в s.

В теории графов нечётные графы On — это семейство симметричных графов с высоким нечётным обхватом, определённых на некоторых семействах множеств. Они включают и обобщают графы Петерсена.

Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).

В теории графов графами Пэли (названы в честь Раймонда Пэли) называются плотные неориентированные графы, построенные из членов подходящего конечного поля путём соединения пар элементов, отличающихся на квадратичный вычет. Графы Пэли образуют бесконечное семейство конференсных графов, поскольку тесно связаны с бесконечным семейством симметричных конференсных матриц. Графы Пэли дают возможность применить теоретические средства теории графов в теории квадратичных вычетов и имеют интересные свойства.

В теории графов графом-циклом называется граф, состоящий из единственного цикла, или, другими словами, некоторого числа вершин, соединённых замкнутой цепью. Граф-цикл с n вершинами обозначают как Cn. Число вершин в Cn равно числу рёбер и каждая вершина имеет степень 2, то есть любая вершина инцидентна ровно двум рёбрам.

В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества.

В теории графов мультиграфом (или псевдографом) называется граф, в котором разрешается присутствие кратных рёбер (их также называют «параллельными»), то есть рёбер, имеющих те же самые конечные вершины. Таким образом, две вершины могут быть соединены более чем одним ребром (тем самым мультиграфы отличаются от гиперграфов, в которых каждое ребро может соединять любое число вершин, а не в точности две).

В теории графов графом без клешней называется граф, который не содержит порождённых подграфов, изоморфных K1,3 (клешней).

В теории графов графом пересечений называется граф, представляющий схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.

Источник

Действительно, при подсчете данной суммы каждое ребро считается дважды: при определении степени одного конца и при определении степени другого конца. 1, то это несвязный граф. Граф, состоящий только из изолированных вершин (в котором k(G)=|V|, r(G)=0), называется вполне несвязным.

Пример 3.9 Граф на рисунке имеет две компоненты связности.

Вершина графа, удаление которой увеличивает число компонент связности, называется разделяющей или точкой сочленения.

Ориентированный граф G(V,E) является слабо связным (слабым), если симметричное замыкание множества E определяет связный граф (иными словами, если после замены всех дуг графа G ребрами полученный граф будет связным). Ориентированный граф является сильно связным (сильным), если для любой пары вершин u,vÎV существует ориентированный путь из u в v (т.е. из любой вершины графа достижимы все его остальные вершины). Если для любой пары вершин по крайней мере одна достижима из другой, то такой граф является односторонне связным, или односторонним. Граф, состоящий из одной вершины, по определению считается сильно связным.

Ñ Множества вершин связных компонент образуют разбиение множества вершин графа.

Граф G’(V’,E’) называется подграфом графа G(V,E): G’(V’,E’) Í G(V,E), если V’Í V и E’Í E, причем каждое из ребер E’ инцидентно только вершинам из V’.

Если G’Í G и множества вершин этих графов не равны, как и множества ребер, то подграф G’ является собственным подграфом графа G (Прим. 3.10, б).

Если множества вершин этих графов совпадают и в графе G’ нет циклов, то G’ называется остовным подграфом (остовом, каркасом) графа G (т.е. он содержит все вершины исходного графа и некоторый поднабор его ребер).

Ñ Очевидно, что остов существует в каждом графе. Для его получения нужно удалить «лишние» ребра, разрушив циклы в каждой связной компоненте.

Остовный подграф для графа G можно построить не единственным образом. В общем, если (n,m)-граф G имеет k компонент связности, то для получения его остова из графа необходимо удалить (m–n+k) ребер.

Пример 3.10 (4,6)-граф G (а), его подграфы (б, в), причем б) – собственный подграф; 2 различных каркаса (г, д). Удаление ребер для получения остовного подграфа: (m–n+k) = 6 – 4 + 1 = 3. Þ из исходного графа требуется удалить 3 ребра (так, чтобы сохранились все вершины исходного графа и не стало циклов).

3.3 Виды графов и операции над ними

3.3.1 Тривиальные и полные графы

Наиболее простое строение имеют пустые и полные графы.

Граф, состоящий из одной вершины, называется тривиальным. Граф, в котором нет ребер, называется пустым (т.е. пустой граф состоит из одних изолированных вершин).

Граф, состоящий из простого цикла с k вершинами, обозначается C_k. Например, C₃ – треугольник, C₄ – квадрат.

Граф с n вершинами называется полным, если любые две его вершины смежны. Такой граф обозначается K_n, он имеет максимально возможное число ребер, равное n×(n–1)/2.

Пример 3.11

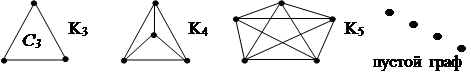Ñ Очевидно, что в пустом графе все вершины изолированные, а в полном степень каждой вершины на 1 меньше порядка графа: deg(v)=n–1 «vÎV.

Полный направленный орграф называется турниром.

Утверждение:

Всякий полный граф является регулярным; обратное же не верно. Для подтверждения достаточно рассмотреть квадрат, который является регулярным графом (степени всех вершин одинаковы и равны 2), но не является полным.

Полный граф G(V,E) соответствует универсальному бинарномуотношению E на множестве вершин V (т.е. «u,vÎV (u,v)ÎE – любые два элемента (вершины) связаны этим отношением).

3.3.2 Двудольные графы

Двудольный граф (или биграф, или четный граф) – это граф G(V,E) такой, что множество вершин разбито на два непересекающихся подмножества V₁ и V₂: V₁ÈV₂=V, V₁ÇV₂=Æ так, что любое ребро соединяет вершину из V₁ с вершиной из V₂. Тогда множества V₁ и V₂ называются долями графа G.

Если граф содержит все ребра, соединяющие множества V₁ и V₂, то он называется полным двудольным графом. Если |V₁|=m и |V₂|=n, то полный двудольный граф обозначается K_m,n.

Пример 3.12 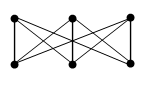На рисунке показан полный двудольный граф K_3,3.

Теорема 3.1 Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Двудольные графы удобны для представления бинарных отношений между элементами двух разных типов, например: множества <исполнители>и <виды работ>. Тогда отношением E может быть «данный исполнитель может выполнять данную работу».

3.3.3 Плоский (планарный) граф

Граф называется планарным, если он может быть изображен на плоскости так, что вершинам соответствуют различные точки плоскости, а линии, соответствующие ребрам, не пересекаются. Геометрическая фигура, являющаяся изображением планарного графа, называется плоским графом.

Говорят, что плоский граф допускает правильную укладку на плоскости.

К рассмотрению планарных графов сводятся такие задачи, как задача о раскраске карт, задача о проектировании коммуникаций, и т.д.

Любая правильная укладка связного графа порождает разбиение плоскости на отдельные области (грани). Такое разбиение называется плоской картой.

Внутренней гранью плоского связного графа называется конечная область плоскости, ограниченная замкнутым маршрутом и не содержащая внутри себя ни вершин, ни ребер графа. Этот маршрут называется границей грани. Часть плоскости, состоящая из точек, не принадлежащих ни графу и ни одной из его внутренних граней, называется внешней гранью.

Для любой плоской карты имеет место формула Эйлера: n – m + r = 2, где n – число вершин, m – число ребер, r – число областей карты (включая внешнюю область).

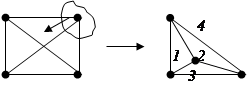
Пример 3.13 Полный двудольный граф K_3,3. и полный граф K₅ не являются плоскими.
Граф K₄ является планарным: см. рисунок. 1,2,3 – его внутренние грани, 4 – внешняя грань.

3.3.4 Направленные орграфы и сети

Если в графе ориентировать все ребра, то получится орграф, который называется направленным. Направленный граф не имеет симметричных пар ориентированных ребер (т.е. в нем не может быть одновременно дуг (u,v) и (v,u)).

Если в орграфе полустепень захода некоторой вершины равна нулю, то такая вершина называется источником; если нулю равна полустепень исхода, то такая вершина называется стоком. Направленный орграф с одним источником и с одним стоком называется сетью.

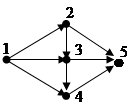
Пример 3.14 Граф на рисунке является сетью, вершина 1 – источником, а вершина 5 – стоком.

3.3.5 Операции над графами

С помощью различных операций можно строить графы из более простых, переходить от одного графа к более простому, разбивать графы на более простые и т.д. Операции могут быть одноместными и двуместными. Рассмотрим эти операции в порядке возрастания их сложности (начнем с одноместных).

1. Дополнением графа G₁(V₁,E₁) называется граф G₂(V₂,E₂), у которого множество вершин такое же, как у исходного графа, а множество ребер представляет собой дополнение до множества E₁: V₂=V₁, E=`E<sub>1</sub> =V<sub>1</sub>´V<sub>1</sub>\E<sub>1</sub>. Вершины графа G<sub>2</sub> смежны только в том случае, когда они не смежны в исходном графе. Обозначение: `G₁(V₁,E₁). Дополнение графов есть дополнение отношений.

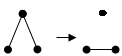
Пример 3.15 Дополнение к полному графу – пустой граф. Другой пример показан на рисунке.

2. Удаление вершины v из графа G₁(V₁,E₁) (при условии vÎV₁): вершина v удаляется из множества V₁, а из множества ребер удаляются ребра, инцидентные этой вершине: V = V₁\<v>, E= E₁\<e = (v₁,v₂) | v₁ = v или v₂ = v>. Обозначение: G = G₁(V₁,E₁)–v.

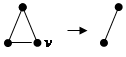
4. Удаление ребра e из графа G₁(V₁,E₁) (при условии eÎE₁): из множества ребер удаляется ребро e: V = V₁, E= E₁ \ <e>; его вершины сохраняются. Обозначение: G = G₁(V₁,E₁)–e.

Пример 3.17 K₂ – e =`K₂.

6. Отождествление вершин v₁,v₂ графа G₁(V₁,E₁): замена этой пары новой вершиной v, причем все ребра, которые вели в удаленные вершины, заменяются ребрами, ведущими в v. Если эти вершины были смежными, то их отождествление называется стягиванием ребра.

Пример 3.18 (4,4)-граф после стягивания ребра превратился в K₂.

7. Стягивание подграфа А графа G₁(V₁,E₁) (при условии AÌV₁): из множества вершин удаляется множество A и заменяется новой вершиной v, все ребра, которые вели в вершины из А, заменяются ребрами, ведущими в v. V = V₁ \ A È <v>, E= E₁ \ <e = (u,v) | uÎA или vÎ A>È<e = (u,v) | uÎГ(A)\A>. Обозначение: G = G₁(V₁,E₁)/A.

8. Подразбиение ребра графа G₁(V₁,E₁): удаление ребра и добавление новой вершины, которая соединяется ребром с каждой вершиной удаленного ребра.

9. Размножение вершины v графа G₁(V₁,E₁) (при условии vÎV₁, v’ÏV₁): во множество вершин добавляется вершина v’, во множество ребер – ребра, соединяющие новую вершину v’ с вершиной v и со всеми смежными с ней вершинами. V = V₁ È <v’>, E = E₁ È <(v,v’)> È <e = (u,v’) | uÎГ + (v)>. Обозначение: G = G₁(V₁,E₁)­v.

10. Объединением графов G₁(V₁,E₁) и G₂(V₂,E₂) (при условии, что их множества вершин, как и множества ребер, не пересекались) называется граф G(V,E), в котором V = V₁ÈV₂, E = E₁ÈE₂. Обозначение: G = G₁ÈG₂.

Пример 3.21 `K_3,3.= C₃ÈC₃. Любой граф является объединением своих компонент связности.

11. Соединением графов G₁(V₁,E₁) и G₂(V₂,E₂) (также при условии, что их множества вершин и множества ребер не пересекались) называется граф G(V,E), в котором V = V₁ÈV₂, E= E₁ÈE₂È<e=(v₁,v₂) | v₁Î V₁, v₂Î V₂>. Иными словами, строится объединение графов и добавляются ребра, соединяющие графы G₁(V₁,E₁) и G₂(V₂,E₂). Обозначение: G = G₁+G₂.

12. Произведением графов G₁(V₁,E₁) и G₂(V₂,E₂) (также при условии, что их множества вершин и множества ребер не пересекались) называется граф G(V,E). В нем V = V₁×V₂, и вершины (u₁,u₂) и (v₁,v₂) смежны только в том случае, если либо u₁=v₁ и u₂ смежна с v₂, либо u₂=v₂ и u₁ смежна с v₁. Обозначение: G = G₁×G₂.

Пример 3.23

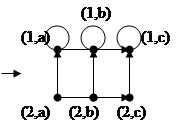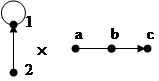Операции над графами могут использоваться для построения графов с заданными свойствами.

Деревья являются простейшим классом графов. Для них выполняются многие свойства, которые не всегда выполняются для обычных графов. Кроме того, деревья широко применяются в программировании при различного рода обработке данных, в частности, в алгоритмах сортировки, кодирования и т.п. Подробно алгоритмы работы с деревьями будут рассматриваться позднее в других курсах, а сейчас только краткое знакомство.

Дерево – это связный граф без циклов. Несколько деревьев (или несвязный граф без циклов) составляют лес. Таким образом, дерево является компонентой связности леса.

1. Любые две вершины в дереве связаны единственной простой цепью.

2. При удалении любого ребра дерева нарушается его связность.

3. Число вершин в дереве на единицу больше числа ребер.

Ориентированные (упорядоченные) деревья используются для представления различного рода иерархических отношений. Они обладают следующими дополнительными свойствами:

1. Существует единственный узел, у которого полустепень захода равна нулю – корень дерева.

2. Полустепень захода всех остальных узлов равна 1.

3. Каждый узел достижим из корня.

4. Узлы дерева с нулевой полустепенью исхода принято называть листьями.

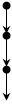
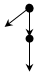
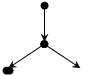
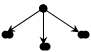
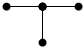
Пример 3.24 Свободные (а) и ориентированные (б) деревья с 4 узлами.
а) б)

3.4 Представление графов в ЭВМ

3.4.1 Требования к представлению графов

Чтобы задать граф, нужно каким-либо способом описать множество его вершин, множество его ребер, а также указать, какие вершины и ребра инцидентны (или смежны), т.е. задать отношение инцидентности (смежности).

Рассмотрим несколько способов представления графа в ЭВМ. Они различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается по потребностям конкретной задачи.

Напоминание: число вершин графа обозначаем через n, а число ребер – через m. Характеристика M(n,m), приведенная для каждого представления, означает требуемый для него объем памяти.

Ñ Указанные представления пригодны для графов и орграфов, а после некоторой модификации – для псевдографов, мультиграфов и гиперграфов.

Все представления будем иллюстрировать на конкретных примерах графа G и орграфа D (см. рисунок.).

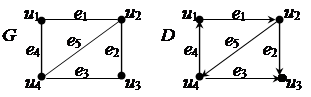
3.4.2 Способы представления графа

1) Матрица смежности.

Матрица смежности A(G’) графа (орграфа) – это квадратная матрица размера n´n, у которой для любых i,j Î<1,2,…,n> элемент в i-й строке и j-м столбце равен 1, если i-я и j-я вершины соединены ребром (дугой с началом в вершине i), и равен 0 в противном случае.

Память M(n,m)=O(n 2 ).

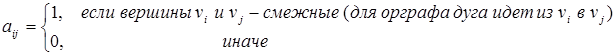
Фактически это уже знакомая нам матрица бинарного отношения. Очевидно, что матрица смежности неориентированного графа является симметричной, элементы главной диагонали равны нулю, а количество единиц в каждой строке равно степени вершины, которой соответствует эта строка. По матрице смежности легко построить диаграмму графа.

Матрица смежности орграфа, не являющегося мультиграфом, не может быть симметричной, т.к. при ее составлении вершины орграфа играют различные роли.

Пример 3.25 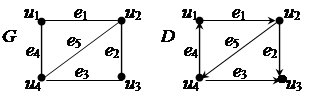Матрицы смежности для заданных графа G и орграфа D

Ñ В матрице смежности мультиграфа или псевдографа число, находящееся на пересечении i-й строки и j-го столбца, совпадает с числом ребер, соединяющих вершины i и j, при этом каждая петля считается двумя ребрами.

Пример 3.26 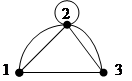Псевдограф, изображенный на рисунке, имеет матрицу смежности следующего вида:

2) Матрица инцидентности.

Другой способ задать граф – определить матрицу инцидентности (или инциденций) I(G), имеющую n строк и m столбцов, элементы которой задаются следующим образом:

Для ориентированного графа:

Пример 3.27 Матрицы инцидентности для заданных графа G и орграфа D

Очевидно, что в каждом столбце матрицы инцидентности только два элемента отличны от 0 (или один, если ребро является петлей), т.к. ребро может быть инцидентно не более чем двум вершинам (а столбец соответствует ребру). Поэтому матрица содержит много нулей и такой способ описания неэкономен. M(n,m)=O(n×m).

3) Списки смежности.

Граф представляется с помощью списочной структуры (списка смежности), отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин. Элемент списка представлен структурой с двумя полями: номер вершины и указатель. Для неориентированных графов M(n,m)=O(n+2m), для орграфов M(n,m)=O(n+m).

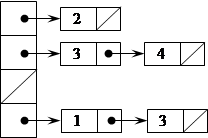
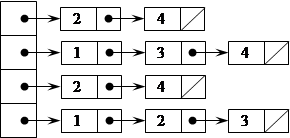
Пример 3.28 Списки смежности для заданных графа G и орграфа D:

4) Массив ребер (дуг).

Отношение инцидентности можно задать также списком ребер графа. Каждая строка этого списка соответствует ребру, в ней записаны номера вершин, инцидентных ему. M=O(2m).

Пример 3.29 Представление с помощью массива ребер (дуг) для заданных: графа G (левый столбец) и орграфа D (правый столбец). В массиве перечислены ребра (дуги) путем указания инцидентных им вершин.

По списку ребер графа легко построить матрицу инцидентности, т.к. каждое ребро этого списка соответствует столбцу матрицы, а номера вершин в каждом элементе списка – это номера строк матрицы инцидентности, элементы в которых равны 1. Для орграфа координата начала – номер строки, где стоит
–1, а координата конца – номер строки, где стоит 1.

Обход графа – это некоторое систематическое перечисление его вершин (ребер). Среди всех обходов наиболее известны поиск в глубину и в ширину. Алгоритмы такого поиска лежат в основе многих алгоритмов на графах.

При поиске используется некоторая структура данных Т, в которую помещаются вершины графа. Для обозначения пройденных вершин заводят дополнительный массив пометок этих вершин.

Поиск основывается на следующих действиях.

1. Сначала все вершины считаются неотмеченными.

2. Выбирается любая вершина (начало поиска), заносится в структуру данных Т и помечается.

3. Следующие действия выполняются в цикле до тех пор, пока структура Т не станет пустой:

– из структуры данных Т выбирается вершина u;

– она выдается в качестве очередной пройденной вершины;

– перебираются все вершины из Г(u), и все те, которые не помечены, тоже заносятся в структуру Т и помечаются.

Если Т – это стек (LIFO), то обход называется поиском в глубину (т.е. первым делом из структуры Т извлекается вершина, попавшая туда последней). Если Т – это очередь (FIFO), то обход называется поиском в ширину. При поиске в глубину находятся более длинные пути.

Теорема 3.2 Если граф G связен и конечен, то поиск в ширину или поиск в глубину обойдет все вершины графа по одному разу.

Доказательство. 1. Единственность обхода. Обходятся только вершины, попавшие в Т. Для помещения в Т выбирают только неотмеченные вершины; при попадании в Т вершина отмечается Þ » вершина будет обойдена по 1 разу.

2. Завершаемость алгоритма. Всего в Т может попасть не более m вершин; на » шаге одна вершина удаляется из Т Þ алгоритм stop не >, чем через m шагов.

Пример 3.33 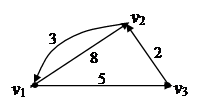Найдем матрицу кратчайших расстояний для графа.
v₁ v₂ v₃

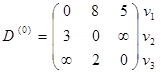
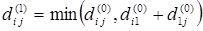
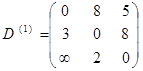
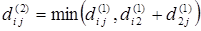
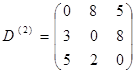
Элементы матрицы D (1) находим по правилу . Первая строка и первый столбец не меняются. Получаем . Элементы матрицы D (2) находим по правилу . Без изменений второй столбец и вторая строка. .
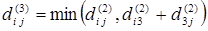
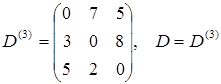
Элементы матрицы D (3) находим по правилу . . Каждый из элементов (i,j) матрицы D равен наименьшему расстоянию между вершинами v_i и v_j.

3.5.3 Минимальный остов

Эта задача возникает при проектировании линий электропередач, трубопроводов, дорог и т.д., когда требуется заданные центры (вершины графа) соединить некоторой системой каналов связи таким образом, чтобы любые два центра были связаны непосредственно или через другие каналы, и чтобы общая длина (стоимость) каналов связи была минимальной.

Для постановки и решения задачи дадим некоторые определения.

Вес остовного дерева взвешенного графа равен сумме весов, приписанных его ребрам. Минимальным остовным деревом называется остовное дерево графа с минимальным весом.

Математическая формулировка задачи: во взвешенном связном графе G(V,E) найти минимальное остовное дерево T(V,E’).

Рассмотрим алгоритм Крускала (Краскала?) решения этой задачи. Идея алгоритма состоит в том, чтобы постепенно формировать дерево Т(V,E’), выбирая ребра с наименьшим весом так, чтобы не возникало циклов.

Первоначально множество Е’ пустое, V – множество вершин графа, Т пустое. Два следующих действия выполняются до тех пор, пока это возможно.

1) Выбрать ребро минимального веса в исходном графе G, не принадлежащее множеству Е’, так, что его добавление в Е’ не создает цикла в дереве Т.

2) Добавить это ребро во множество ребер Е’.

3.5.4 Эйлеровы графы

Цикл в графе называется эйлеровым, если он содержит все ребра графа. Связный граф, в котором существует эйлеров цикл, называется эйлеровым графом. Эйлеровой цепью (или путем) является цепь (путь), которая включает все ребра (дуги) графа по одному разу. Собственная эйлерова цепь – это эйлерова цепь, которая не является эйлеровым циклом.

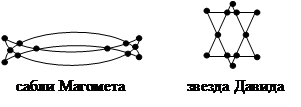
Эйлеров граф можно нарисовать, не отрывая карандаша от бумаги. Известные примеры эйлеровых графов приведены на рисунке.

Дата добавления: 2017-06-02 ; просмотров: 3864 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник