Линейное время работы алгоритма означает что
Оценка сложности алгоритмов, или Что такое О(log n)
Авторизуйтесь
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
20–22 декабря, Онлайн, Беcплатно
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
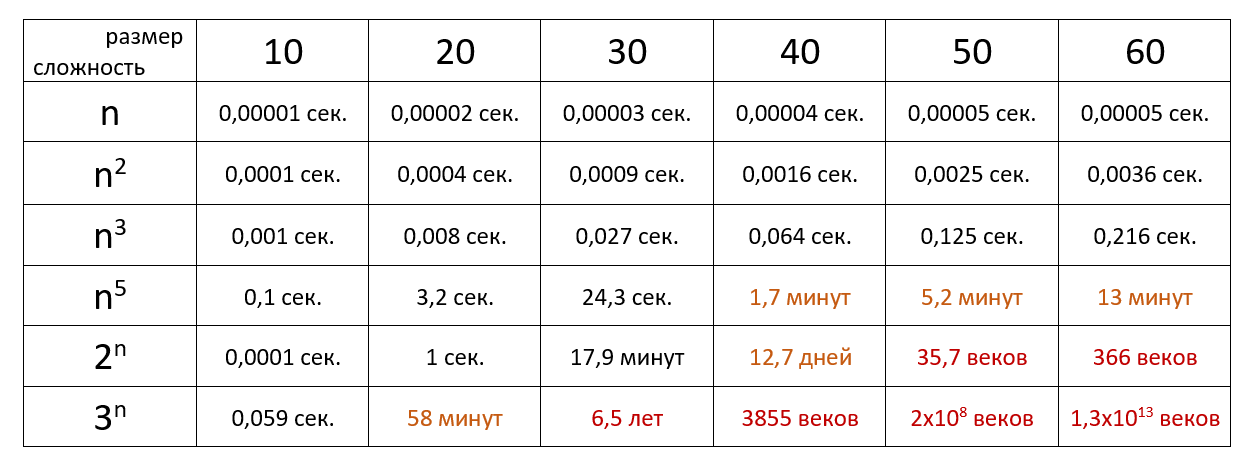
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
«О» большое: объяснение для тех, у кого нет диплома по информатике
Перевод статьи «Big-O For The Non-CS Degree».
Вам когда-нибудь было любопытно, почему одни алгоритмы работают быстрее других? Да, я раньше тоже как-то не задумывался над этим, а зря. Объяснить это различие в скорости помогает «О» большое.
Что такое это ваше «О» большое?
Это способ измерить, сколько по времени будет выполняться алгоритм и насколько хорошо он масштабируется относительно размера набора данных. В общем, «О» большое служит для измерения эффективности алгоритмов.
Допустим, у нас есть список из 15 человек и мы хотим найти в этом списке всех людей, чье имя начинается на «Т». Для сортировки можно использовать разные алгоритмы, причем все они будут отличаться по уровню сложности. И некоторые из них будут более производительными, чем другие.
А теперь представьте, что имен у нас не 15, а миллион. Как вы думаете, насколько такой прирост данных повлияет на производительность алгоритмов? Ответ на этот вопрос можно найти при помощи нотации «О» большое.
«О» большое бывает разным:
Давайте рассмотрим каждый из вариантов.
O(1) — постоянное время
Если у алгоритма постоянная временная сложность, значит, размер передаваемых данных никак не влияет на его производительность. Время выполнения останется неизменным, какой бы набор данных вы ему ни передали. То есть, это может быть список из 5 элементов, а может быть и из тысячи — не важно. Алгоритм с такой нотацией очень масштабируемый.
Допустим, у нас есть массив чисел и мы хотим найти второй элемент в этом списке. Не важно, насколько длинный наш список: поиск второго элемента всегда будет занимать одинаковое время.
Оба вызова функции будут выполнены за одинаковое время, несмотря на то, что один список больше другого.
O(log n) — логарифмическое время
Если у алгоритма логарифмическая временная сложность, это значит, что время выполнения будет зависеть от логарифма размера входящих данных. Хорошим примером может послужить бинарный поиск. Вы последовательно делите набор данных надвое, пока не достигнете нужной точки.
В примере, приведенном ниже, мы перебираем в цикле список чисел и проверяем, равен ли элемент на серединной позиции определенному значению. Если нет, мы отделяем половину чисел, выбираем новую серединную позицию и проверяем снова. Это продолжается, пока мы не найдем нужное нам число или пока в массиве не кончатся числа.
O(n) — линейное время
Линейная временная сложность алгоритма означает, что время его работы находится в прямой зависимости от размера входящих данных. Если количество элементов наборе данных растет, пропорционально растет и время работы.
Посмотрите на пример, приведенный ниже. Мы используем цикл for для вывода на экран каждого элемента массива. Чем больше элементов, тем дольше работает алгоритм.
Если бы мы добавили еще один элемент в массив junkFood, время работы функции возросло бы пропорционально.
O(n log n) — линейно-логарифмическое время
Если временная сложность алгоритма описывается линейно-логарифмической функцией, то, как вы можете догадаться, она занимает промежуточное положение между линейной и логарифмической сложностью. В таком алгоритме тоже применяется подход «разделяй и властвуй», как в алгоритмах с логарифмической сложностью. Но здесь набор данных сначала разбивается на подсписки, состоящие максимум из двух элементов (т. е., на пары).
В нашем примере мы взяли список из 20 элементов. Эти элементы сначала будут разбиты попарно, на 10 подсписков. И здесь вступает в игру «линейная» часть функции. Когда все элементы разбиты попарно, мы сортируем каждую отдельную пару, а затем последовательно объединяем отсортированные пары, продолжая сортировать получившийся результат. Пример алгоритма с линейно-логарифмической временной сложностью — сортировка слиянием.
O(n^2) — квадратичное время
Квадратичная временная сложность — это когда производительность алгоритма прямо пропорциональна размеру входных данных в квадрате. Проще говоря, это линейная временная сложность в квадрате.
Если, к примеру, в нашем наборе данных есть 2 элемента, за время работы алгоритма будет выполнено 4 операции. Если в наборе 4 элемента, то операций будет 16. При 6 элементах будет 36 операций, и так далее.
В нашем примере мы применяем алгоритм сортировки пузырьком, имеющий квадратичную временную сложность. Мы создаем вложенный цикл внутри другого цикла, сортируем наш массив и меняем местами смежные элементы, если они идут в неправильном порядке.
Это очень хороший метод работы для маленьких объемов данных, потому что такой алгоритм легко реализовать. Но при увеличении объема входных данных время работы будет расти экспоненциально. Очевидно, что подобные решения не годятся для масштабирования.
O(2^n) — экспоненциальное время
Экспоненциальную временную сложность мы можем наблюдать в алгоритмах, где количество вычислений удваивается при добавлении каждого нового элемента в набор данных. Так происходит, например, в брутфорс-решениях с использованием рекурсии. На маленьких наборах данных все работает отлично, но с увеличением числа элементов в наборе время выполнения может выйти из-под контроля.
Хорошим примером может служить рекурсивный расчет чисел Фибоначчи — такой, как в коде, приведенном ниже.
O(n!) — факториальное время
Факториальная временная сложность — это когда количество вычислений в алгоритме прирастает факториально в зависимости от размера набора данных. Это, пожалуй, наихудший тип временной сложности, потому что количество операций возрастает до астрономических пределов даже при небольшом увеличении набора данных.
Как видите, число операций ужасно растет при каждом добавлении элемента в набор.
Хорошим примером алгоритма с факториальной временной сложностью может послужить простая рекурсивная функция. Эта функция принимает число в качестве входных данных и умножает его на факториал числа, меньшего на единицу. (В общем, стандартная функция для вычисления факториала числа, переданного в качестве инпута, — прим. ред. Techrocks). Как видите, время работы функции при незначительном увеличении входных данных растет просто катастрофически.
Итоги
Когда ищете алгоритмическое решение задачи, важно учитывать временную сложность выбранного алгоритма. Не все алгоритмы одинаково производительны: некоторые могут быть эффективнее других в зависимости от величины обрабатываемого объема данных. А для сравнения эффективности алгоритмов применяется нотация большого «О».
Что такое временная сложность алгоритма?
Когда в детстве меня учили умножать числа, мне говорили, что смысл умножения в том, чтобы короче записать сумму. Например, 4 * 3 это то же, что 4 + 4 + 4.
Сведение умножения к сумме — самый простой, наивный алгоритм умножения. А теперь я возьму мой рабочий ноут и попробую перемножить этим способом какие-нибудь большие числа, например, 4 * 10000000000:
Если я попробую посчитать то же самое на калькуляторе, то замечу, что лаптоп отрабатывает заметно медленнее, несмотря на то, что он мощнее. Почему? Потому что для умножения чисел существует несколько алгоритмов, а я выбрала самый неэффективный из них. Ещё есть, например, метод Карацубы, или алгоритм на основе преобразования Фурье. В калькуляторах обычно используется второй, и он требует значительно меньше операций, чем наивный.
Как понять, быстро ли работает алгоритм? Можно попробовать измерить время напрямую:
Но мы обнаружим, что скорость зависит от производительности машины, от ее архитектуры и загруженности в момент выполнения программы. Поэтому физическое время никак не поможет нам оценить эффективность алгоритма.
Чтобы уйти от физических свойств вычислителя, используют понятие сложности. Асимптотическая сложность алгоритма — это то, как изменяется время исполнения в зависимости от объема входных данных. В этом определении намеренно не учитывается то, на каком устройте выполняется алгоритм: это может быть компьютер, калькулятор или даже человек. Такой абстрактный вычислитель называют машиной Тьюринга.
При этом разделяют сложность алгоритма в худшем и лучшем случае. Представьте, что мы хотим проверить, есть ли в списке число 42. Мы проверяем первый элемент на равенство 42, второй, третий… В лучшем случае первый элемент окажется искомым. В худшем — последний. Поэтому обычно рассматривают сложность алгоритма в наилучшем, наихудшем случае, и в среднем. Как правило, пессимистическая оценка самая интересная из всех, потому что позволяет планировать объем ресурсов.
Временную сложность алгоритма в худшем случае выражают с использованием нотации «O» большое. В этом случае из рассмотрения исключают члены меньшего порядка и говорят об изменении используемых ресурсов при стремлении размера входа к бесконечности. Например, если время, которое нужно алгоритму для выполнения работы, для всех входов длины n не превосходит 5n^3 + 3n, то асимптотическая временная сложность равна O(n^3).
Рассмотрим несколько примеров
Время, которое не зависит от объема входных данных, или постоянное время. За постоянное время можно получить элемент массива по индексу или добавить элемент в связный список.
Алгоритм, в котором мы идём по списку, чтобы узнать, есть ли в нем значение 42, в худшем случае требует O(n) операций, где n — длина списка. Такую же сложность имеет сравнение строк, потому что по сути оно тоже требуют обхода всей строки.
O(log n)
Проверить, есть ли значение 42 в списке, можно быстрее, чем за O(n), если список отсортирован. Тогда можно проверить на равенство элемент из середины списка. Если он равен 42, то останавливаемся. Если больше — значит, слева можно не искать, там значения только меньше. Будем продолжать проверку, выбирая каждый раз элемент из середины оставшегося отрезка. Этот алгоритм называют бинарным поиском и он имеет логарифмическую сложность, потому что количество вариантов уменьшается каждый раз на 2, как функция, обратная степенной (она же логарифм).
O(n log n)
Можно показать, что большинство алгоритмов сортировки имеют сложность n log(n). За время n log(n) работают сортировка слиянием, кучей, и быстрая сортировка. Еще есть теорема, которая говорит, что если сортировка основана на сравнении элементов, то быстрее, чем за n log(n) отсортировать элементы не получится.
За время n^2 работает обход двумерного массива, это можно представить себе как обход таблицы n * n. И ещё за это же время работают некоторые не очень эффективные по времени алгоритмы сортировки, например, сортировка пузырьком.
Для разработчика важно иметь интуицию насчет временной сложности алгоритмов, потому что за счет неэффективности вычислений можно загубить производительность самого мощного железа, как это случилось, когда калькулятор побил мой мощный ноутбук. Поэтому этой науке уделяется большое внимание в разработке. 95%, что на собеседовании вам предложат алгоритмическую задачу и попросят оценить время выполнения вашего решения.
Если вы хотите углубиться в теорию алгоритмов, то я советую специализацию Алгоритмы и структуры данных на Курсере. Теория здесь изложена доступно и в курсе есть задачи, чтобы набить руку. А еще есть Стенфордский учебник по теории сложности, он написан замечательным языком и в нем прекрасные примеры.