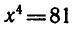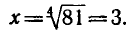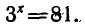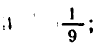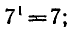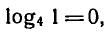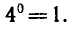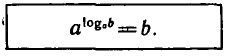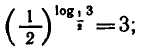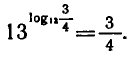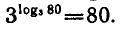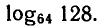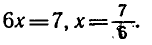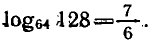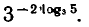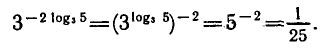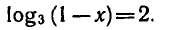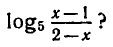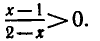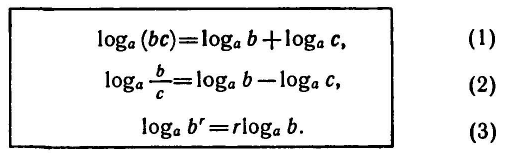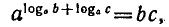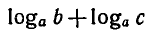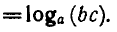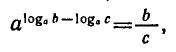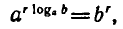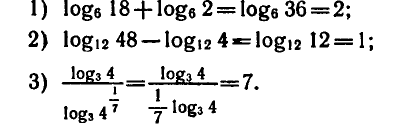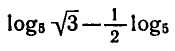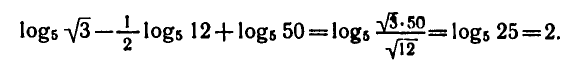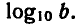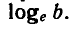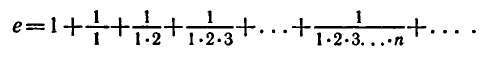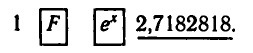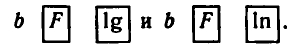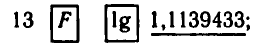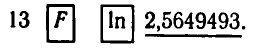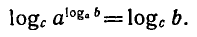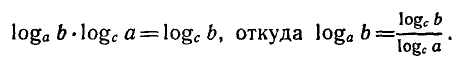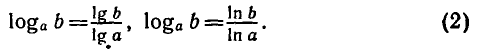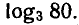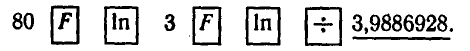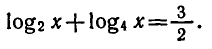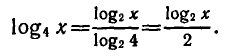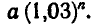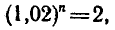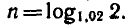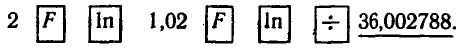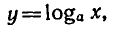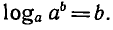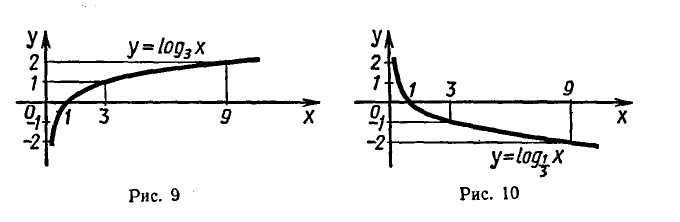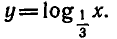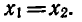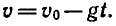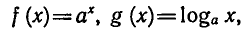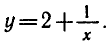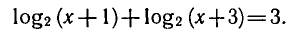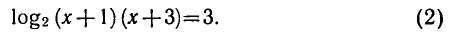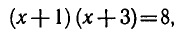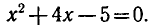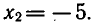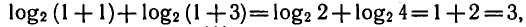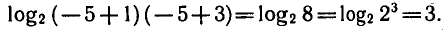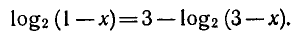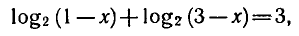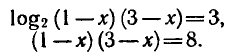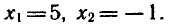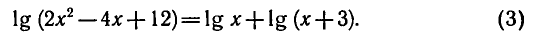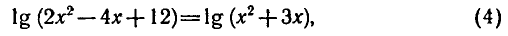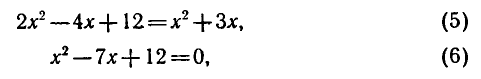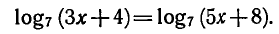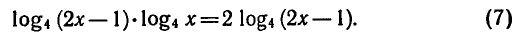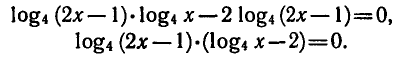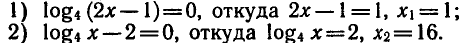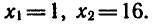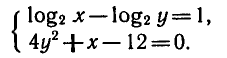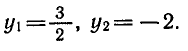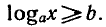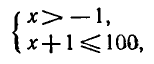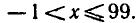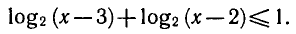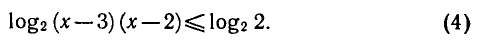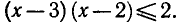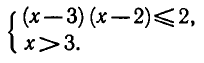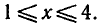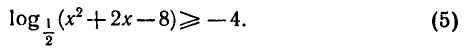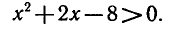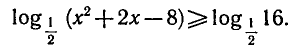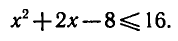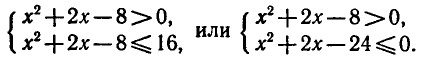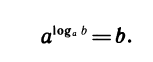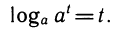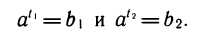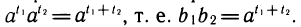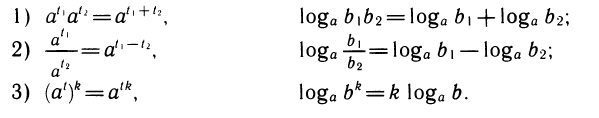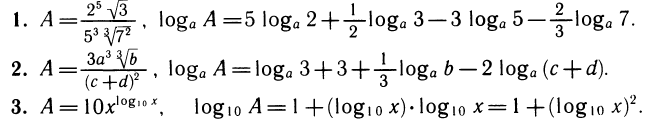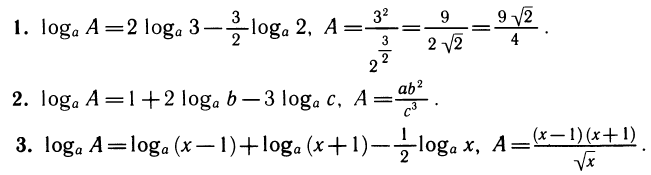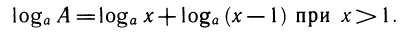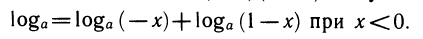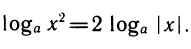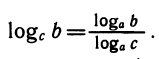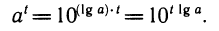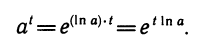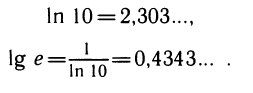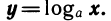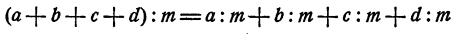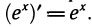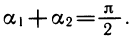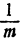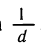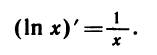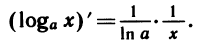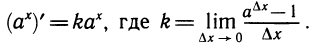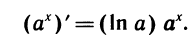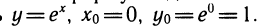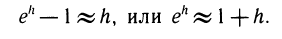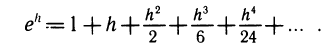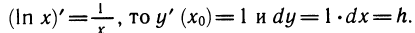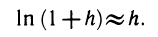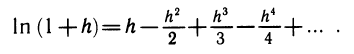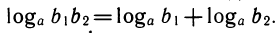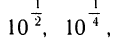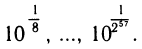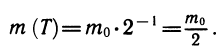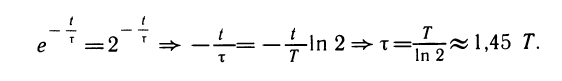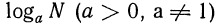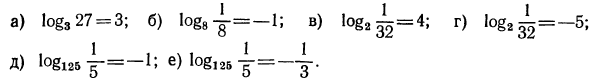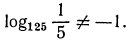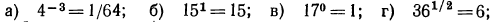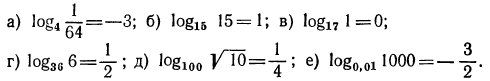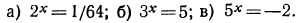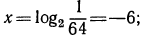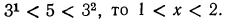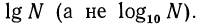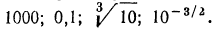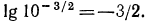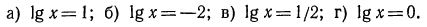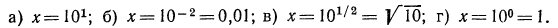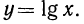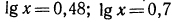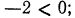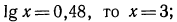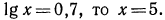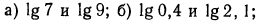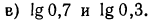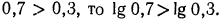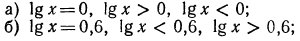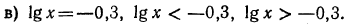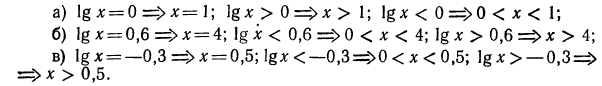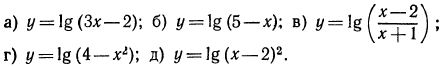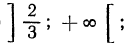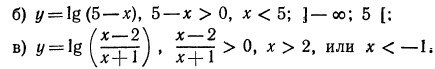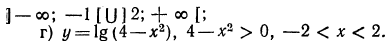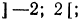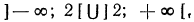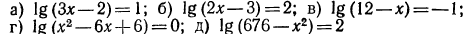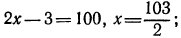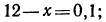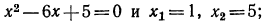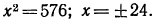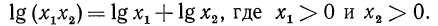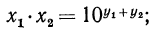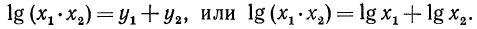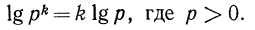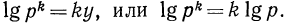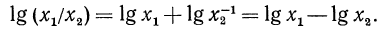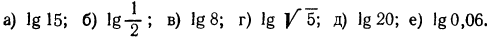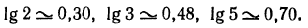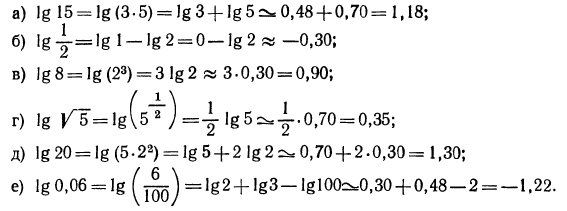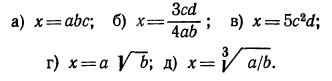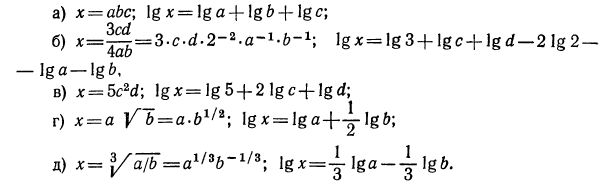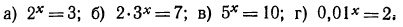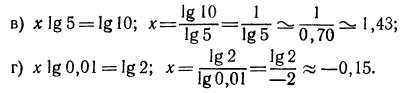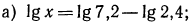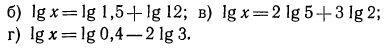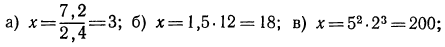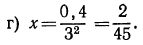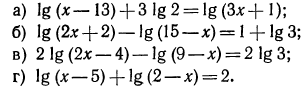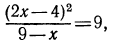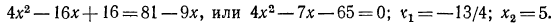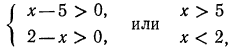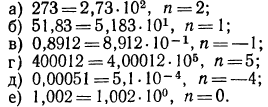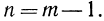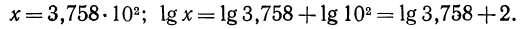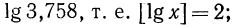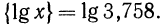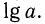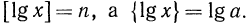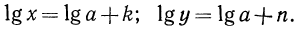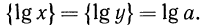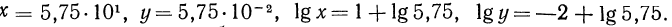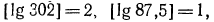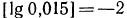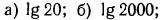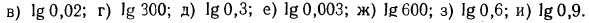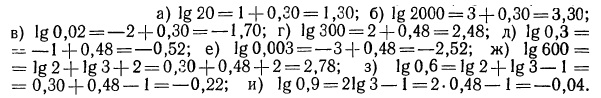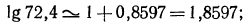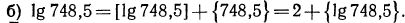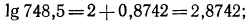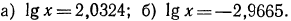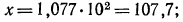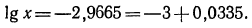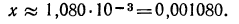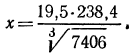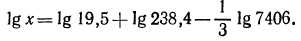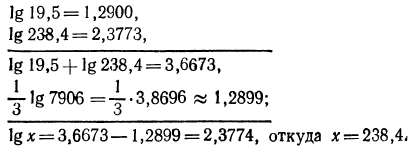Логарифмическая функция возрастает на области определения при условии что основание логарифма
Логарифмическая функция возрастает на области определения при условии что основание логарифма
График функции имеет следующий вид:
Рассмотрим свойства функции:
Примеры решения задач
Задание 1.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции y = log2x. Для этого найдем значения функции при x = 


| x |  |  |  | 1 | 2 | 4 | 8 |
| y(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = log2x возрастает на всей области определения D(y)=R+, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. C осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем больше основание a (если a > 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задание 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции 



| x |  |  |  | 1 | 2 | 4 | 8 |
| y(x) | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y. Функция 
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. С осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем меньше основание a (если 0
Все данные функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти обасть определеления функции:
Решение
Область определения данной функции задается следующим неравенством:
Решим это линейное неравенство:
Логарифм определен, если подлогарифмическая функция является положительной, то есть искомая область определения: D(y): (x-1)(x+5) > 0.
Решим полученное уравнение методом интервалов. Для этого найдем нули каждого из сомножителей:
Наносим их на координатную прямую и определяем знак неравенства на каждом из полученных промежутков.
Что такое логарифмическая функция? Определение, свойства, решение задач
Раздел логарифмов занимает огромное значение в школьном курсе «Математического анализа». Задания для логарифмических функций построены на иных принципах, нежели задачи для неравенств и уравнений. Знание определений и основных свойств понятий логарифм и логарифмическая функция, обеспечат успешное решение типовых задач ЕГЭ.
Определение понятия логарифм
Прежде чем приступить к объяснению, что представляет собой логарифмическая функция, стоит обратиться к определению логарифма.
Разберем конкретный пример: а log a x = x, где a › 0, a ≠ 1.
Основные свойства логарифмов можно перечислить несколькими пунктами:
Логарифмирование
Логарифмированием называют математическую операцию, которая позволяет с помощью свойств понятия найти логарифм числа или выражения.
Функция логарифма и ее свойства
Логарифмическая функция имеет вид
Сразу отметим, что график функции может быть возрастающим при a › 1 и убывающим при 0 ‹ a ‹ 1. В зависимости от этого кривая функции будет иметь тот или иной вид.
Приведем свойства и способ построения графиков логарифмов:
Построить обе разновидности графиков очень просто, рассмотрим процесс на примере
Для начала необходимо вспомнить свойства простого логарифма и ее функции. С их помощью нужно построить таблицу для конкретных значений x и y. Затем на координатной оси следует отметить полученные точки и соединить их плавной линией. Эта кривая и будет являться требуемым графиком.
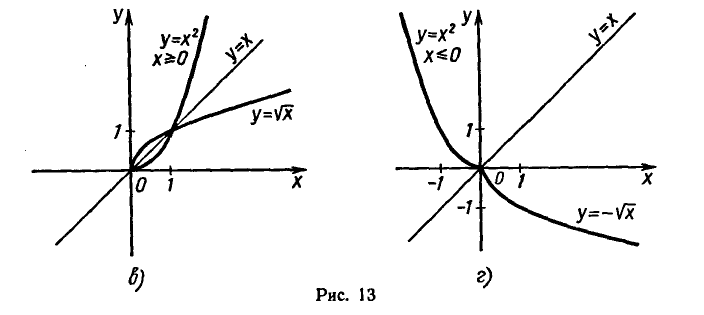
Очевидно, что обе линии являются зеркальным отражением друг друга. Построив прямую y = x, можно увидеть ось симметрии.
Для того, чтобы быстро найти ответ задачи нужно рассчитать значения точек для y = log2x, а затем просто перенести начала точки координат на три деления вниз по оси OY и на 2 деления влево по оси OX.
В качестве доказательства построим расчетную таблицу для точек графика y = log2(x+2)-3 и сравним полученные значения с рисунком.
Как видно, координаты из таблицы и точек на графике совпадают, следовательно, перенос по осям был осуществлен правильно.
Примеры решения типовых задач ЕГЭ
Большую часть тестовых задач можно разделить на две части: поиск области определения, указания вида функции по рисунку графика, определение является ли функция возрастающей/убывающей.
Для быстрого ответа на задания необходимо четко уяснить, что f(x) возрастает, если показатель логарифма а › 1, а убывает – при 0 ‹ а ‹ 1. Однако, не только основание, но и аргумент может сильно повлиять на вид кривой функции.
Задание 1
F(x), отмеченные галочкой, являются правильными ответами. Сомнения в данном случае вызывают пример 2 и 3. Знак «-» перед log меняет возрастающую на убывающую и наоборот.
Ответ: 3,4,5.
Задание 2
Ответ: 4.
Данные типы заданий считаются легкими и оцениваются в 1- 2 балла.
Задание 3.
Определить убывающая или возрастающая ли функция и указать область ее определения.
Так как основание логарифма меньше единицы, но больше нуля – функция от x является убывающей. Согласно свойствам логарифма аргумент также должен быть больше нуля. Решим неравенство:
Ответ: область определения D(x) – интервал (50; + ∞).
Задание 4.
Ответ: 3, 1, оси OX, направо.
Подобные задания классифицируются как средние и оцениваются в 3 – 4 балла.
Задание 5. Найти область значений для функции:
Из свойств логарифма известно, что аргумент может быть только положительным. Поэтому рассчитаем область допустимых значений функции. Для этого нужно будет решить систему из двух неравенств:
Итак, искомый промежуток находится в пределе интервала (-4; 8), при других x становится невозможным вычислить значение одного из данных логарифмических выражений.
Согласно свойствам логарифмической функции сумма логарифмов с одинаковым основанием равна логарифму произведения их аргументов.
Графиком функции y = – x 2 + 4x + 32 является парабола, схематический график которой представлен ниже.
Точка A является экстремумом графика, в ней y принимает наибольшее значение. Координаты точки A (m; n) вычисляются по формулам, приведенным на рисунке. Высчитаем n для заданной параболы.
Наибольшее значение ymax = 36. Так как основание логарифма в примере больше 1, то функция будет возрастающей, и достигнет наибольшего значения при максимальном аргументе. Узнаем максимум для F(y):
Наименьшего значения в конкретном примере нет, поэтому ОДЗ для f(x) = log3(x+4)+ log3(8-x) является следующий интервал (- ∞; 2log36).
Подобные задачи можно отнести к категории «сложно» и оценивать не менее 4 баллов за правильный ответ.
Логарифмическая функция в математике с примерами решения и образцами выполнения
Пример:
Найти положительный корень уравнения
( По определению арифметического корня имеем-
Пример:
Решить уравнение
Запишем данное уравнение так: 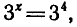
Лаплас Пьер Симон (1749— 1827)— французский математик, физик и астроном, адъюнкт Французской Академии Наук. После Великой Французской революции принимал активное участие в реорганизации системы образования. Важнейшие направления его исследований — математика, небесная механика и математическая физика. Один из создателей теории вероятностей.
так как 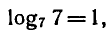
так как
Определение логарифма можно кратко записать так:
Это равенство справедливо при b > 0, а > 0, 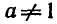
называют основным логарифмическим тождеством.
Например, 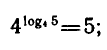
С помощью основного логарифмического тождества можио
показать, например, что 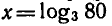
В самом деле,
Действие нахождения логарифма числа называют логарифмированием.
Пример:
Вычислить
Обозначим 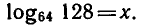
Так как 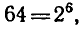
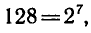
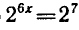
откуда
Ответ.
Пример:
Вычислить
Используя свойства степени и основное логарифмическое равенство, находим:
Пример:
Решить уравнение
Но определению логарифма 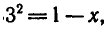
Пример:
При каких значениях х существует
Так как основание логарифма 5 > 0 и 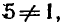
существует тогда и только тогда, когда
Получено неравенство, находим 1 Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а>0, 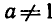
По основному логарифмическому тождеству
1) Перемножая равенства (4) и (5), получаем:
откуда по определению логарифма
Формула (1) доказана.
2) Разделив равенства (4) и (5), получим:
откуда по определению логарифма следует формула (2).
3) Возводя основное логарифмическое тождество 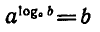
в степень с показателем r, получаем:
откуда по определению логарифма следует формула (3). •
Приведем примеры применения формул (1) — (3):
Пример:
Вычислить 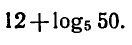
Применяя формулы (1) — (3), находим:
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы
(таблицы логарифмов). Логарифмы вычисляют также с помощью
микрокалькулятора. И в том и в другом случае находятся только
десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо
Натуральным логарифмом числа называют логарифм этого числа по основанию e, где е — иррациональное число, приближенно равное 2,7. При этом пишут ln e вместо
Иррациональное число е играет важную роль в математике
и ее приложениях. Число е можно представить как сумму:
Вычисление числа е на микрокалькуляторе проводится по
программе:
Вычисления на микрокалькуляторе lg b и ln b проводятся
соответственно по программам:
Например, вычисляя lg 13, получаем:
вычисляя ln 13, получаем:
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить
логарифмы чисел по любому основанию. Для этого используется
формула перехода от логарифма по одному основанию к
логарифму по другому основанию:
Докажем справедливость формулы (1).
Запишем основное логарифмическое тождество 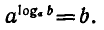
Возьмем от обеих его частей логарифмы по основанию с:
Используя свойство логарифма степени, получаем:
Из формулы (1) при с = 10 и с = е получаются формулы
перехода к десятичным и натуральным логарифмам:
Пример:
С помощью микрокалькулятора МК-54 вычислить
1) С помощью десятичных логарифмов:
2) С помощью натуральных логарифмов:
Ответ. 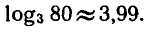
Формула перехода от одного основания логарифма к другому
иногда используется при решении уравнений.
Пример:
Решить уравнение
По формуле перехода
Поэтому уравнение принимает вид 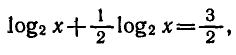
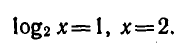
Пример:
Двухпроцентный вклад в Сбербанк, равный
а рублям, через п лет становится равным 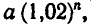
трехпроцентный вклад становится равным
Через сколько лет каждый из вкладов удвоится?
1) Для первого вклада 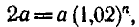
2. Вычисления проведем на МК-54:
2) Для второго вклада 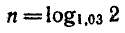
такова:
Ответ. По первому вкладу приближенно через 36 лет, а
по второму — через 23,5 года.
Логарифмическая функция и ее график
В математике и ее приложениях часто встречается
логарифмическая функция
где а — заданное число, а > 0, 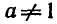
Логарифмическая функция обладает следующими свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение 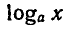
2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа
b есть такое положительное число х, что 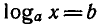
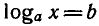
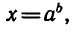
Пользуясь основным логарифмическим
тождеством, условие 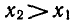

Пусть 0 1, то функция 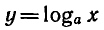
Это следует из того, что функция 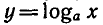
значение, равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если а > 1, и убывающей, если 0 1, и на рисунке 8, если 0 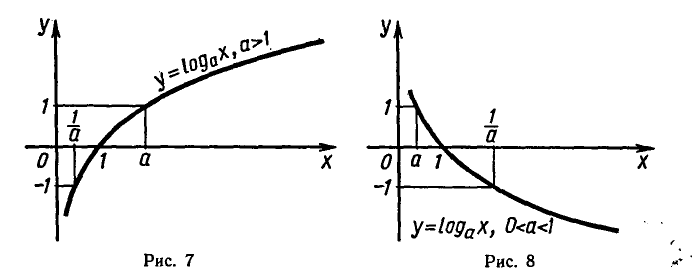
На рисунке 9 изображен график функции 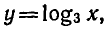
Отметим, что график любой логарифмической функции 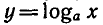
Теорема:
Если 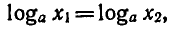
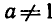
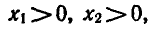
Предположим, что 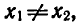
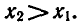


0 0 и возрастает, то неравенство 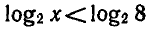
Ответ.
Обратная функция
Известно, что зависимость скорости v от времени t движения
тела, брошенного вверх с начальной скоростью 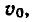
формулой
Из этой формулы можно найти обратную зависимость — времени от скорости: 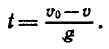
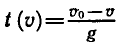
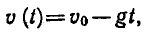
Рассмотрим теперь показательную и логарифмическую
функции. Обозначим символом f(х) показательную функцию,
a g (х) — логарифмическую функцию:
где а — заданное число, а > 0, 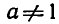
Решим уравнение 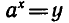
логарифма 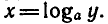
получим логарифмическую функцию 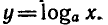
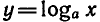
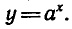
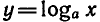
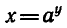
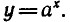
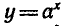
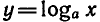
Вообще если функция y = f(x) задана формулой, то для
нахождения обратной функции нужно решить уравнение
f (x) = у относительно х и затем поменять местами х и у.
Если уравнение f(x)= y имеет более чем один корень, то
функции, обратной к y = f (x), не существует.
Например, функция 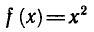
уравнение 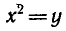
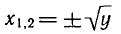
у > 0.
Если функцию 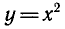
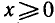
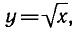
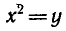
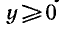
Пример:
Найти функцию, обратную к функции
Решая это уравнение относительно х, получаем 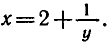
Заменив х на у и у на х, находим
В этой задаче область определения функции 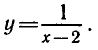
множество действительных чисел, не равных 2, а множество ее значений — все действительные числа, не равные 0. График этой
функции изображен на рисунке 11.
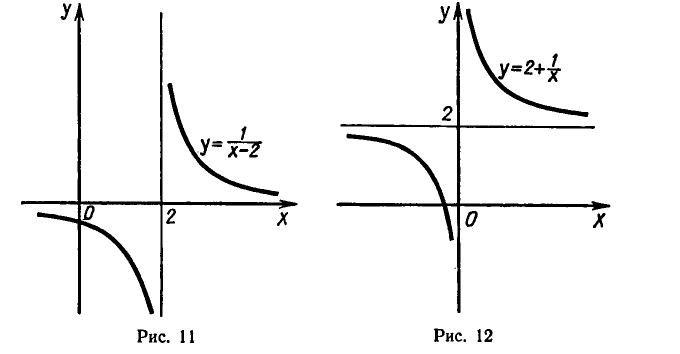
Для обратной функции 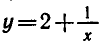
множество действительных чисел, не равных 0, а множество значений — все действительные числа, не равные 2. График обратной функции изображен на рисунке 12.
Вообще область определения обратной функции совпадает
с множеством значений исходной функции, а множество
значений обратной функции совпадает с областью определения
исходной функции.
Можно показать, что если функция имеет обратную, то
график обратной функции симметричен графику данной
функции относительно прямой у = х.
Примеры графиков взаимно обратных функций показаны на
рисунке 13.
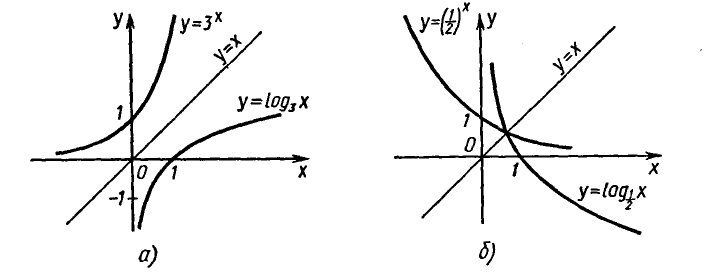
Логарифмические уравнения
Пример:
Предположим, что х — такое число, при котором равенство ( 1 ) является верным, т. е. х — корень уравнения ( 1 ).
Тогда по свойству логарифма верно равенство
Из этого равенства по определению логарифма получаем:
откуда 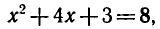
Последнее равенство верно, если 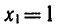
т. е. х = 1 — корень уравнения ( 1 ).
Заметим, что х = — 5 является корнем уравнения (2), так
как
Получилось, что число х = 1 является корнем обоих уравнений
( 1 ) и (2), а число х = — 5 не является корнем уравнения (1 ), но является корнем уравнения (2). Таким образом, при переходе от уравнения (1) к уравнению (2 ) корень х = 1 сохранился и появился посторонний корень х = —5. В этом случае уравнение (2) называют следствием уравнения (1 ).
Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Отметим, что в уравнении, которое является следствием
данного, не всегда появляются посторонние корни; важно лишь
то, чтобы корни исходного уравнения не терялись.
В большинстве случаев, как и в задаче 1, уравнения решаются постепенным переходом к более простым уравнениям,
которые являются следствием исходного уравнения. В таких
случаях после нахождения корней необходима их проверка.
Пример:
Перенесем логарифм из правой части в левую;
Решая это уравнение, получаем
Число 
как при x = 5 левая и правая части уравнения теряю т смысл.
Проверка показывает, что число х = — 1 является корнем
исходного уравнения.
Ответ. х = — 1. ▲
Пример:
По свойству логарифмов
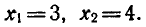
являются корнями исходного уравнения.
Ответ. 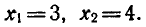
Проверкой можно убедиться в том, что числа 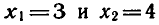
(4) и (5). Все эти уравнения других корней не имеют. Такие
уравнения называют равносильными.
Уравнения, имеющие одно и то же множество корней,
называют равносильными.
В частности, два уравнения, не имеющие корней, являются
равносильными.
Отметим, что любое из двух равносильных уравнений является следствием другого.
Большинство уравнений, с которыми вы встречались в курсе
алгебры, решались с помощью перехода от данного уравнения
к равносильному. Так решались уравнения первой степени с
одним неизвестным, квадратные уравнения, показательные
уравнения.
Напомним, что уравнение заменяется ему равносильным при
следующих преобразованиях:
любой член уравнения можно переносить из одной части
в другую, изменив его знак на противоположный;
обе части уравнения можно умножить или разделить на
одно и то же число, не равное нулю.
Однако не при любом преобразовании уравнение заменяется
на равносильное. Например, при возведении обеих частей
уравнения 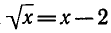
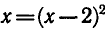
Пример:
Приравнивая выражения, стоящие под знаком логарифма,
получаем:
откуда х = — 2. Выполняя проверку, убеждаемся, что при х = — 2
левая и правая части исходного уравнения не имеют смысла.
Ответ. Корней нет.
Здесь посторонний корень появился потому, что при переходе
от равенства логарифмов к равенству чисел не было учтено
требование, чтобы эти числа были положительными.
Рассмотренные примеры логарифмических уравнений
показывают, что при их решении с использованием свойств логарифмов получаются уравнения, которые являются следствиями исходного. Поэтому необходима проверка, которая позволяет
обнаружить посторонние корни. ▲
Пример:
Преобразуем данное уравнение:
Приравнивая каждый из множителей левой части уравнения
к нулю, получаем:
Проверка показывает, что оба значения х являются корнями
исходного уравнения.
Ответ.
Отметим, что если обе части уравнения (7) разделить на
выражение 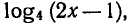
Вообще при делении обеих частей уравнения на выражение, содержащее неизвестное, может произойти потеря корней.
Поэтому уравнение, обе части которого содержат общий
множитель, решают переносом всех членов в одну часть и
разложением на множители.
При решении уравнений главное не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.
Пример:
Решить систему уравнений
Из первого уравнения выразим х через 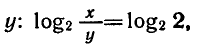
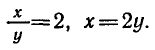
получим 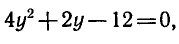
Найдем значения х : 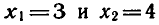
что 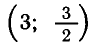
решение.
Ответ.
Логарифмические неравенства
При изучении логарифмической функции рассматривались
неравенства вида 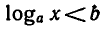
Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений.
Пример:
Правая часть данного неравенства имеет смысл при всех значениях x, а левая часть — при x + 1 > 0, т. е. при х > — 1.
Промежуток х > — 1 называют областью определения неравенства (1). Так как логарифмическая функция с основанием
10 возрастающая, то неравенство ( 1 ) при условии x + 1 > 0
выполняется, если 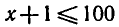
образом, неравенство ( 1 ) равносильно системе неравенств
т. е. неравенство ( 1 ) и система (2) имеют одно и то же множество решений. Решая систему (2), находим
Пример:
Логарифмическая функция определена при положительных значениях аргумента, поэтому левая часть неравенства имеет смысл при х — 3 > 0 и х — 2 > 0.
Логарифмическая функция с основанием 2 возрастающая. Поэтому при х > 3 неравенство (4) выполняется, если
Таким образом, исходное неравенство (3) равносильно системе неравенств
Решая первое неравенство этой системы, получаем 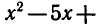
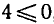
Пример:
Область определения неравенства находится из условия
Неравенство (5) можно записать в следующем виде:
Так как логарифмическая функция с основанием 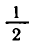
убывающей, то для всех х из области определения неравенства
получаем:
Таким образом, исходное неравенство (5) равносильно системе неравенств
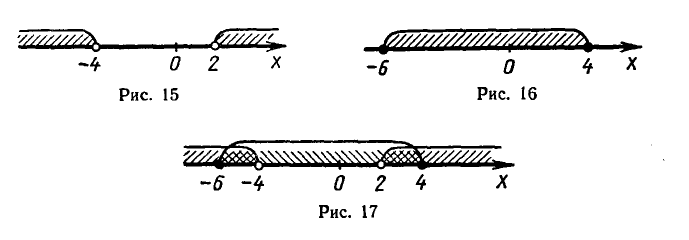
Решая первое квадратное неравенство, получаем х 2 (рис. 15). Решая второе квадратное неравенство, получаем 
мы выполняются одновременно при 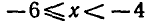
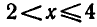
Ответ.
Определение:
Логарифмом числа а по основанию b называется показатель степени, в которую надо возвести а, чтобы получить число b.
В качестве основания мы будем всегда брать положительное число а, отличное от 1.
В записи b = 
Можно сказать, что формулы 
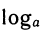
Подставляя в равенство 
Представляя в равенстве 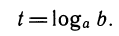
Свойства логарифмов
Теорема:
Верны следующие тождества, выражающие свойства логарифмов:
1)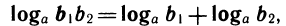
2) 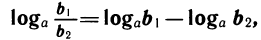
3) 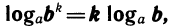
Доказательство:
Свойства логарифмов выводятся из свойств степеней с помощью основного логарифмического тождества, выражающего определение логарифма. Выведем для примера первое свойство.
Обозначим 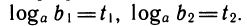
Перемножим эти равенства: 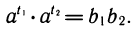
По определению логарифма t1+ t2 = 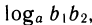
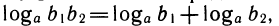
Свойства степеней и логарифмов тесно связаны между собой. Они фактически выражают одно и то же, только один раз мы обращаем внимание на поведение самих степеней, а другой — на поведение показателей:
С помощью свойств логарифмов можно логарифмировать выражения, составленные с помощью операций умножения, деления и возведения в степень.
Примеры.
Иногда приходится искать выражение по его логарифму. Такую операцию называют потенцированием.
Примеры:
Замечание. Запись 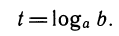
Если же х
Аналогично 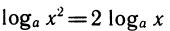
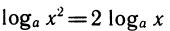
Модуль перехода
В вычислениях в качестве основания а часто берется число а=10. В то же время зачастую необходимы вычисления степеней и логарифмов с разными основаниями. Возникает вопрос: как связать между собой степени и логарифмы с разными основаниями?
Пусть дана степень b = 

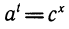
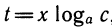
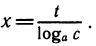
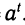
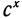
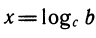
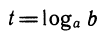
Выведенную формулу называют формулой перехода от одного основания логарифма к другому.
Таким образом, мы видим, что при изменении основания значения логарифмов изменяются пропорционально. Коэффициент пропорциональности 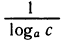
Отметим простые следствия выведенной формулы:
1) 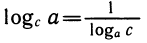
2) 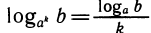
3) 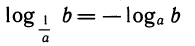
С помощью логарифмов все степени можно привести к одному основанию. Если в качестве основания берется число a =10, то соответствующие логарифмы обозначаются знаком lg и называются десятичными. Можно записать:
Если в качестве основания берется число е, то соответствующие логарифмы обозначаются знаком ln и называются натуральными:
Значения модулей перехода от десятичных логарифмов к натуральным и наоборот таковы:
Исследование логарифмической функции
Определение:
Логарифмической функцией называется функция вида
Напомним, что в качестве основания логарифмов выбирается число а> 0, отличное от 1.
Основные свойства логарифмической функции (схема X).
Графики функций 
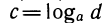
Так как точки Р (с; d) и Q (d; с) симметричны относительно прямой у = х (рис. 109), то симметричны и графики показательной и логарифмической функций.
Вместо логарифмических функций с произвольным основанием удобно рассматривать функции вида у = с ln х. Так как 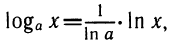
Функция у = ln х растет с ростом х, однако медленнее, чем любая степенная функция вида 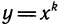
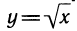
Производная логарифмической функции
Рассмотрим две функции у = 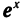
Пусть a1 и а2 — углы, образованные проведенными касательными с осью абсцисс. Из рисунка 109 ясно, что
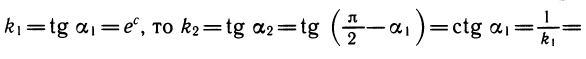
Таким образом, производная функции у = ln х в точке x = d равна
Мы видим, что производная логарифмической функции y = ln х равна степенной функции 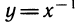
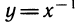
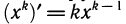
Так как 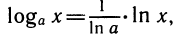
По формулам производной показательной функции 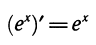
Примеры:
Зная производные экспоненты и логарифма, можно получить приближенные формулы для их вычисления.
Пусть
Разность 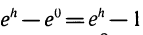
Более точная формула для вычисления экспоненты такова:
Пусть теперь у =lnх. Выберем дго=1, xо = ln l =0. Положим dx = h и вычислим ln (l+h). Найдем dy при xo=1. Так как
(In то y’ (jc0)= 1 и dy= 1 •dx = h.
Заменяя ∆y= ln (1+h) — ln l = ln (l+h), получаем приближенную формулу
Более точная формула для вычисления логарифма такова:
Вычисление логарифмов
Более 300 лет логарифмы использовались для облегчения вычислений. Их основное достоинство — способность сводить умножение к сложению по формуле
Были составлены обширные таблицы логарифмов чисел, с помощью которых можно легко переходить от чисел к их логарифмам и обратно.
Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Бриггса. Генри Бриггс (1561 —1630) с очень большой точностью (16 знаков после запятой) извлек подряд 57 квадратных корней из 10 и получил значения
Комбинируя эти значения, он получил густую сетку чисел с известными десятичными логарифмами: 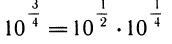
Это огромная работа, и за 300 лет не нашлось никого, кто повторил бы ее. Любопытно, что немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550—1617).
С появлением ЭВМ ситуация переменилась. Умножение по-прежнему выполняется дольше, чем сложение, но логарифмирование требует еще больше времени. Поиск числа в таблице очень дорогая операция для ЭВМ. Поэтому теперь значение логарифмов как инструмента вычисления резко упало, а с распространением калькуляторов оно сходит на нет. С другой стороны, сами по себе логарифмические зависимости легко обрабатываются и используются при вычислениях на ЭВМ. Например, формула xk = exp(k ln x) служит основным средством возведения в степень (кроме k= l, 2, 3) на всех ЭВМ и на калькуляторах.
На современных ЭВМ (и на калькуляторах) значения In х и 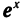
Прикладные примеры
Во вводной беседе мы уже говорили о том, что многие процессы описываются с помощью показательных функций. Почему так происходит, это мы обсудим в следующей главе, а сейчас приведем примеры зависимостей, в которых встречаются экспоненты и логарифмы.
Вычислим значение m при t — Т. Так,
Это означает, что через время Т после начального момента масса радиоактивного вещества уменьшается вдвое. Поэтому число Т называют периодом полураспада. Период полураспада радия равен 1600 лет, урана-238 — 4,5 млрд. лет, цезия-137 —31 год, иода-131 —8 суток.
Закон радиоактивного распада часто записывают в стандартном виде 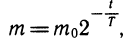
2. Рост народонаселения. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой 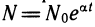
Барометрическая формула. Давление воздуха убывает с высотой (при постоянной температуре) по закону 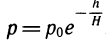
4. Формула Циолковского. Эта формула, связывающая скорость ракеты у с ее массой m, такова: 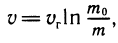
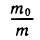
5. Коэффициент звукоизоляции стен измеряется по формуле 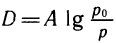
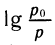
Дополнение к логарифмической функции

Логарифмическая функция
Определение логарифма: Логарифмом числа N по данному основанию а называется такой показатель степени, в который надо возвести основание а, чтобы получить число N; запись
Примеры:
Таким образом, 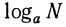
Примеры:
1. Проверить справедливость следующих равенств:
Решение:
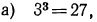
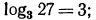
б), г), е) верны; 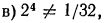
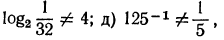
2.Следующие равенства переписать в виде логарифмических равенств:
Решение:
Указать, какие из нижеследующих уравнений имеют решение. Запишите это решение с помощью логарифма:
Решение:
а) Уравнение 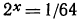
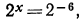
б) Уравнение 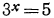
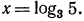
в) Уравнение 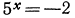
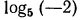
Десятичные логарифмы
Если основанием логарифмов служит число 10, то такие логарифмы называются десятичными. Десятичный логарифм числа N принято обозначать
Примеры:
Найти десятичные логарифмы следующих чисел:
Решение:
Так как 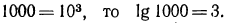
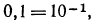
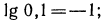
2.Решить следующие уравнения:
Решение:
Функция
Функция 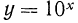
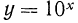
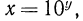
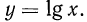
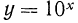
1.Областью определения функции является множество всех положительных чисел.
2.Областью значений функции является множество всех действительных чисел.
Справедливость этих двух свойств вытекает из того факта, что функции 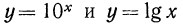
3.Функция 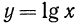
4.При 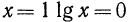
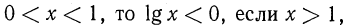
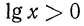
Примеры:
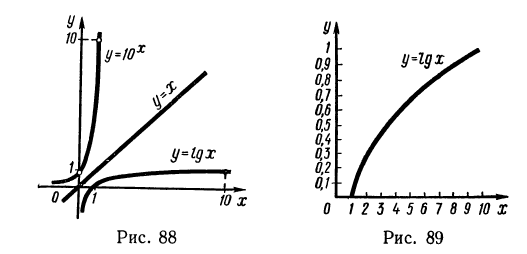
1. На рис. 89 изображен график функции 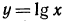
а) найти 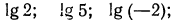
Решение:
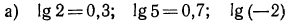
б) если
Если
2.Сравнить значения выражений:
Решение:
а) Функция 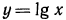
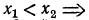
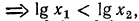
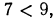
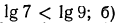
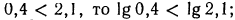
3.Решить уравнения и неравенства:
Решение:
Воспользовавшись изображенным на рис. 89 графиком функции 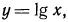
4.Найти область определения функции:
Решение:
При решении этих примеров надо помнить о том, что область определения функции 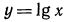
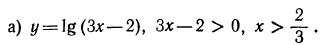
Область определения —объединение двух множеств
Область определения —множество
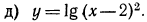
Решение:
а) Так как 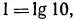
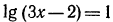
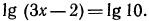
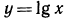
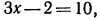
Аналогично решаются и остальные уравнения;
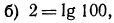
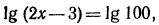
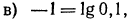
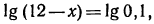
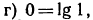
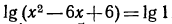
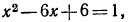
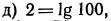
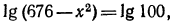
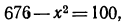
Логарифмирование и потенцирование
Применение логарифмов позволяет во многих случаях значительно упростить вычисления. Чтобы убедиться в этом, прежде всего выясним, как находятся логарифмы произведения, частного, степени и корня.
Теорема:
Логарифм произведения любых двух положительных чисел равен сумме логарифмов множителей, т. е.
Доказательство:
Пусть 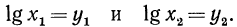
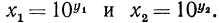
Предлагаем читателю самому доказать, что установленное свойство справедливо для любого числа положительных множителей.
Теорема:
Логарифм степени с положительным основанием равен произведению показателя степени и логарифма ее основания, т. е.
Доказательство:
Пусть 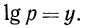
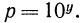
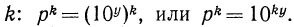
Покажем, что знания этих теорем достаточно для нахождения логарифмов дроби и корня. Действительно, пусть дано выражение 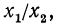
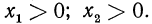
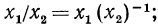
Пусть теперь дано выражение 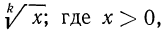
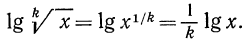
Примеры:
1. Найти приближенные значения следующих логарифмов:
Решение:
Прежде всего, воспользовавшись графиком функции 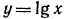
2.Прологарифмировать следующие выражения (буквами обозначены положительные числа):
Решение:
Решение:
а) Прологарифмировав обе части данного равенства, получим 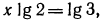
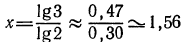
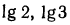
б) в результате логарифмирования имеем равенство 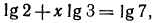
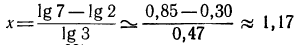
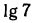
4.Найти x, если:
Решение:
Решение:
а) Потенцируя обе части равенства, получаем уравнение
Сделаем проверку. Подставив в уравнение найденное решение х = 21, получим:
Таким образом, корень данного уравнения x=21;
б) прежде чем потенцировать, заметим, что 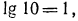
Сделаем проверку: 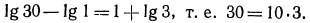
Сделаем проверку. Корень 
Корень x = 5, как легко видеть, удовлетворяет уравнению (Проверьте сами!);
г) уравнение 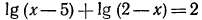
а эта система противоречива и решения не имеет.
Стандартный вид числа. Характеристика и мантисса
Любое положительное число х можно записать в так называемом стандартном виде: 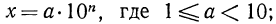
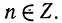
Примеры:
Записать следующие числа в стандартном виде и указать их порядок: а) 273; б) 51,83; в) 0,8912; г) 400012; д) 0,00051; е) 1,002.
Решение:
Легко видеть, что если 


Если же число 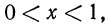
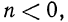
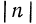
Пример:
Не переходя к стандартному виду записи, найти порядок чисел: а) х = 373,25; б) x: = 0,00085.
Решение:
а) Число 373,25 больше единицы и содержит в целой части три цифры. Следовательно, его порядок n= 2;
б) число 0,00085 меньше единицы и содержит четыре нуля до первой значащей цифры. Следовательно, n =—4.
Пусть х=375,8. Запишем это число в стандартном виде и найдем его логарифм:
Так как 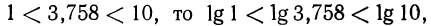
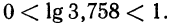
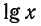
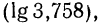
Целая часть логарифма числа называется его характеристикой, а дробная часть — мантиссой.
Теорема:
Характеристика логарифма числа 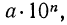
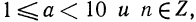
Доказательство:
Пусть 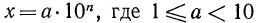
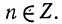
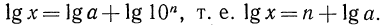
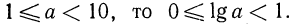
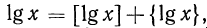
Следствие:
Логарифмы чисел, отличающихся друг от друга только порядком, имеют одну и ту же мантиссу.
Доказательство:
Пусть 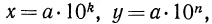
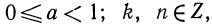
Например, пусть 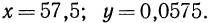
Таким образом, доказанное следствие можно сформулировать иначе: мантисса логарифма числа не зависит от положения запятой в числе.
Примеры:
1. Найти характеристику логарифма числа а) 302;б) 87,5; в) 0,015.
Решение:
Как было доказано Выше, характеристика логарифма числа равна его порядку, а поэтому
2.Зная, что 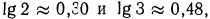
Решение:
Вычисления с помощью таблиц логарифмов
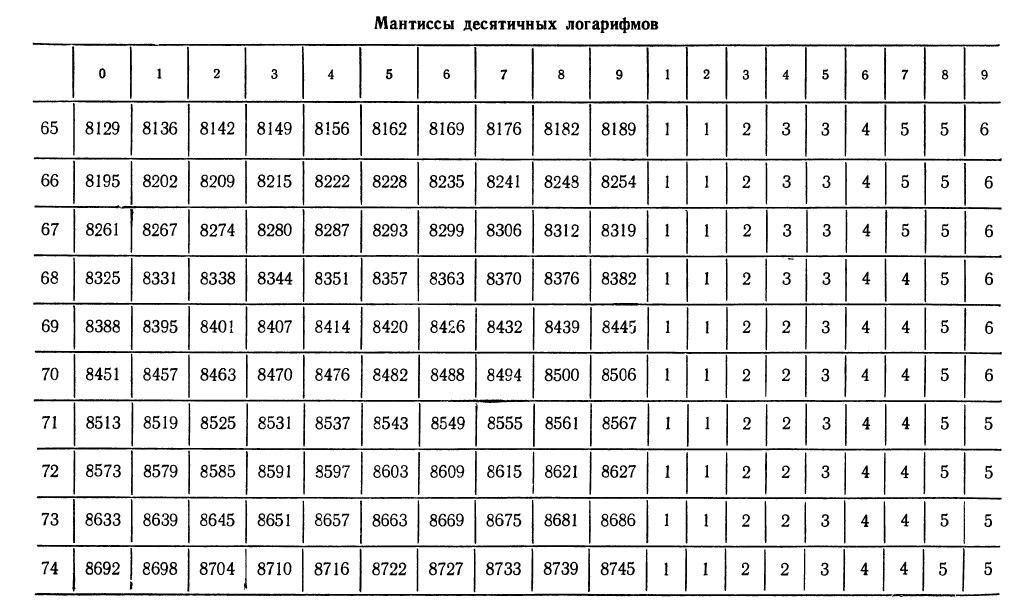
Как известно, характеристика логарифма числа легко находится устно (она равна порядку числа). Значения мантисс приведены в таблице «Четырехзначных математических таблиц» В. М. Брадиса. Приведем часть этой таблицы и укажем как ею пользоваться.
Примеры:
1. Найти логарифмы следующих чисел:
Решение:
а) Характеристика 
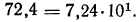
Для отыскания мантиссы мы, прочитав число 8739 на пересечении строки с меткой «74» и столбца с меткой «8», прибавим к этому числу поправку на четвертую цифру. Эта поправка расположена в правой части таблицы на пересечении той же строки и столбца поправок с меткой «5». Поправка равна 3, следовательно, мантисса равна 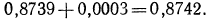
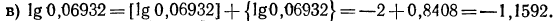
2.Найти x:, если:
Решение:
а) По таблице значений функции 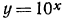
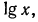
б) представим данный логарифм в виде суммы характеристики и мантиссы:
Мантиссу 0,0335 имеет любое число вида 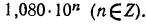
В заключение приведем пример вычисления с помощью таблиц логарифмов.
3.Вычислить значение х, если
Решение:
По таблице логарифмов найдем:
Решение:
а) Характеристика 
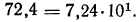
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института