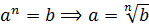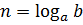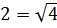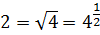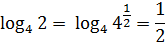Логарифмы для чего они нужны

Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов

Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.

Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.

В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.

Итак, давайте разбираться, что такое логарифм.

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Основные свойства логарифмов

Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:

Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!

Рассмотрим свойства логарифмов на примерах.

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:

log_a 1 = 0 – логарифмический ноль.

Основное логарифмическое тождество

В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.

Вторая формула по сути является просто переформулированным определением логарифма

Разберем применение тождества на примере:

Необходимо найти значение выраженияСначала преобразуем логарифм

Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:

10 примеров логарифмов с решением

1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник

Для чего нужны логарифмы?

Слово «логарифм» многие бывшие ученики общеобразовательных учреждений помнят со школьных уроков математики. Эта тема некоторым из них казалась сложной и непонятной. Не все из них действительно поняли, что такое логарифмы и для чего они нужны. Попробуем разобраться в этом вместе с вами.

Конечно, в математике есть определение этого слова, но оно не всем может показаться понятным. Логарифмирование – это действие, которое обратно возведению в степень. Неподготовленному человеку трудно понять, что означают эти слова, и какая от всего этого польза.

Что же это такое и как с этим можно работать?

Допустим, нужно найти х в уравнении 5 х = 12. В этом случае х будет равен числу, в которое надо возвести 5, чтобы получилось 12. Используя логарифм, этот пример будет звучать так: х равен логарифму 12 по основанию 5. А выгладит уравнение так: х = log₅12. Если произвести вычисление на калькуляторе или компьютере, то получается иррациональное число. Чтобы было легче работать с такими числами, и создали такую математическую конструкцию, как логарифм.

Говоря простым языком, они нужны для упрощения трудных вычислений. Логарифмы обладают важными свойствами, благодаря которым умножение можно заменить простым сложением, а извлечение корня и его возведение в степень можно преобразовать в умножение и в деление.

Применение свойств логарифмов в жизнедеятельности человека

Если логарифмы имеют одинаковое основание, то их сумма равна логарифму произведения, а разность – частного. И получается, что при математических действиях со сложными иррациональными числами, результатом становятся привычные всем натуральные числа. Если основания логарифма разные, то их можно преобразовать по формулам перехода к новому основанию.

Для упрощения подобных вычислений были созданы логарифмические таблицы. С их помощью можно было легко умножать числа, складывая их логарифмы. Более 300 лет такие таблицы расширялись и уточнялись многими математиками. С появлением возможности электронных вычислений, пользоваться логарифмами стало ещё проще. Таблицы теперь используют только в узкоспециализированных сферах.

Свойства логарифмов на практике пригодятся многим людям, занятым на производстве и в научных сферах, в которых необходимы трудоёмкие вычисления. С их помощью можно сравнивать величины, значительно отличающиеся друг от друга. Если вы нарисуете обычный график, на котором отмечены значения 10, 100 и 100 000, то маленькие значения будут практически около ноля. Но логарифмическая линейка позволяет сделать изображение таких чисел более наглядным. С помощью подобных схем часто проводится анализ сравнения шумов, что бывает полезным во многих сферах.

Где можно получить больше информации о свойствах логарифмов?

Пропустили занятие в школе, готовитесь к ЕГЭ или просто интересуетесь математикой? Тогда вам может пригодиться видеоурок на тему «Свойства логарифмов. Логарифм степени», который можно найти, перейдя по ссылке http://interneturok.ru/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/svoystva-logarifmov-logarifm-stepeni.

В рамках занятия преподаватель не только расскажет о формуле логарифма степени, но и докажет её и напомнит некоторые важные свойства логарифмов. Также можно узнать, как использовать свойства логарифма при решении распространенных примеров. Видеоурок дополнен иллюстрированным текстовым конспектом, в котором также можно найти необходимую информацию.

Источник

Что такое логарифм? Зачем нужны логарифмы?

Логарифмы — традиционная головная боль для многих учеников старших классов. Особенно — уравнения и неравенства с логарифмами. Не любят старшеклассники логарифмы почему-то. И поэтому боятся. И совершенно зря.) Ибо сам по себе логарифм — это очень и очень простое понятие. Не верите? Убедитесь сами! В сегодняшнем уроке.

Итак, поехали знакомиться.)

Для начала решим в уме вот такое очень простенькое уравнение:

Это простейшее показательное уравнение. Оно так называется из-за того, что неизвестное икс находится в показателе степени. Даже если вы не в курсе, как решаются показательные уравнения, просто в уме подберите икс так, чтобы равенство выполнилось. Ну же?! Ну, конечно же, х = 2. Два в квадрате — это четыре.)

А теперь я изменю в нём всего одно число. Вот такое уравнение теперь решим:

И снова пробуем подобрать икс…

Что, никак не подбирается? Два в квадрате — это четыре. Два в кубе — это уже восемь. А у нас — пятёрка. Мимо проскочили… Что делать? Только не говорите мне, что нету такого икса! Не поверю.)

Согласитесь, что это как-то несправедливо: с четвёркой уравнение решается в уме, а с пятёркой — уже не решается никак. Математика не приемлет такой дискриминации! Для неё все числа — равноправные партнёры.)

На данном этапе мы можем лишь грубо прикинуть, что икс — какое-то дробное число между двойкой (2 2 = 4) и тройкой (2 3 = 8). Можем даже немного повозиться с калькулятором и приближённо подобрать, найти это число. Но такая возня каждый раз… Согласен, как-то грустно…

Математика решает данную проблему очень просто и элегантно — введением понятия логарифма.

Итак, что же такое логарифм? Вернёмся к нашему загадочному уравнению:

Осмысливаем задачу: нам надо найти некое число х, в которое надо возвести 2, чтобы получить 5. Понятна эта фраза? Если нет, перечитайте ещё раз. И ещё… Пока не осознаете. Ибо это очень важно!

Вот и назовём это загадочное число х логарифмом пятёрки по основанию два! В математической форме эти слова выглядят так:

А произносится эта запись вот так: «Икс равен логарифму пяти по основанию два.»

Ну, вот, собственно, и всё! Мы решили ужасное на вид показательное уравнение!

И всё! Это правильный и совершенно полноценный ответ!

Может быть, вас смущает, что вместо конкретного числа я пишу какие-то непонятные буковки и значки?

Ну что ж, ладно, уговорили… Специально для вас:

x = log₂5 = 2,321928095…

Имейте в виду, что число это никогда не кончается. Да-да! Иррациональное оно…

Вот вам и ответ на вопрос, для чего нужны логарифмы. Логарифмы нам нужны, в первую очередь, для решения показательных уравнений! Таких, которые без логарифмов и не решаются вовсе…

Например, решая показательное уравнение

про логарифмы можно не вспоминать. Сразу ясно, что х = 2.

А вот, решая уравнение, скажем, такое

вы приближённо получите вот такой лохматый ответ:

Зато через логарифм даётся абсолютно точный ответ:

И все дела.) Вот поэтому и пишут логарифмы вместо некрасивых иррациональных чисел. Кому нужен числовой ответ — посчитает на калькуляторе или хотя бы в Excel.) А раньше, когда калькуляторов и компьютеров не было и в помине, существовали специальные таблицы логарифмов. Объёмные и увесистые. Так же, как и таблицы Брадиса для синусов и косинусов. И даже инструмент такой был — логарифмическая линейка. Которая позволяла с хорошей точностью вычислять массу полезных вещей. И не только логарифмы.)

Ну вот. Теперь, незаметно для себя, мы научились решать все показательные уравнения такого зверского типа.

Это всё верные ответы! Ну как? Заманчиво, правда?

А теперь вдумаемся в смысл самой операции нахождения логарифма.

Как мы знаем, на каждое действие математики стараются найти противодействие (т.е. обратное действие). Для сложения это вычитание, для умножения это деление. А какое обратное действие есть для возведения в степень?

Давайте посмотрим. Какие у нас основные действующие фигуры при возведении в степень? Вот они:

b — собственно сама степень.

А теперь подумаем: если нам известна степень (b) и известен показатель этой самой степени (n), а найти надо основание (a), то что мы обычно делаем? Правильно! Извлекаем корень n-й степени! Вот так:

А теперь посмотрим на другую ситуацию: нам снова известна степень (b), но на этот раз вместо показателя n нам известно основание (a), а найти как раз надо этот самый показатель (n). Что делать будем?

Вот тут-то на помощь и приходят логарифмы! Прямо так и пишут:

«Эн» (n) — это число, в которое надо возвести «a», чтобы получить «b». Вот и всё. Вот и весь смысл логарифма. Операция нахождения логарифма — это всего лишь поиск показателя степени по известным степени и основанию.

Простейшие примеры с логарифмами.

А теперь новость не очень хорошая. Если логарифм считается ровно, то его надо считать, да.

Скажем, если где-то в уравнении вы получили

то такой ответ никто не оценит. Надо логарифм посчитать и записать:

А как мы поняли, что log₃9=2? Переводим равенство с математического языка на русский: логарифм девяти по основанию три — это число, в которое надо возвести три, чтобы получить девять. И в какое же число надо возвести тройку, чтобы получить девятку? Ну, конечно! В квадрат надо возвести. То есть, в двойку.)

А чему равен, скажем, log₅125? А в какой степени пятёрка даёт нам 125? В третьей, разумеется (т.е. в кубе)!

Стало быть, log₅125 = 3.

В какую степень надо возвести 7, чтобы получить 7? В первую!

Вот вам и ответ: log₇7 = 1

А вот такой пример как вам?

И в какую же степень надо возвести тройку, чтобы получить единицу? Неужели не догадались? А вы вспомните свойства степеней .) Да! В нулевую! Вот и пишем:

Уловили принцип? Тогда тренируемся:

Ответы (в беспорядке): 1; 3; 5; 0; 4.

Что? Забыли, в какой степени 3 даёт 243? Что ж, ничего не поделаешь: степени популярных чисел надо узнавать. В лицо! Ну, и таблица умножения — надёжный спутник и помощник. И не только в логарифмах.)

Ну вот, совсем простенькие примеры порешали, а теперь шагаем на ступеньку выше. Вспоминаем отрицательные и дробные показатели.)

Решаем вот такой пример:

Мда… И в какую же степень надо возвести четвёрку, чтобы получить 0,25? Так с ходу и не скажешь. Если работать только с натуральными показателями. Но степени в математике, как известно, бывают не только натуральными. Самое время подключить наши знания об отрицательных показателях и вспомнить, что

Стало быть, можно смело записать:

В какую такую степень надо возвести четвёрку, чтобы получить двойку? Для ответа на этот вопрос придётся подключать наши знания о корнях. И вспомнить, что двойка — это корень квадратный из четырёх:

А корень квадратный математика позволяет представить в виде степени! С показателем 1/2. Так и пишем:

Поэтому наш логарифм будет равен:

Ну что, поздравляю! Вот мы с вами и познакомились с логарифмами. На самом примитивном начальном уровне.) И вы сами лично убедились, что они вовсе не так страшны, как, возможно, вам казалось раньше. Но у логарифмов, как и у любых других математических понятий, есть свои свойства и свои особые фишки. О том и о другом (о свойствах и о фишках) — в следующем уроке.

Источник