Ломаная что это определение 2 класс

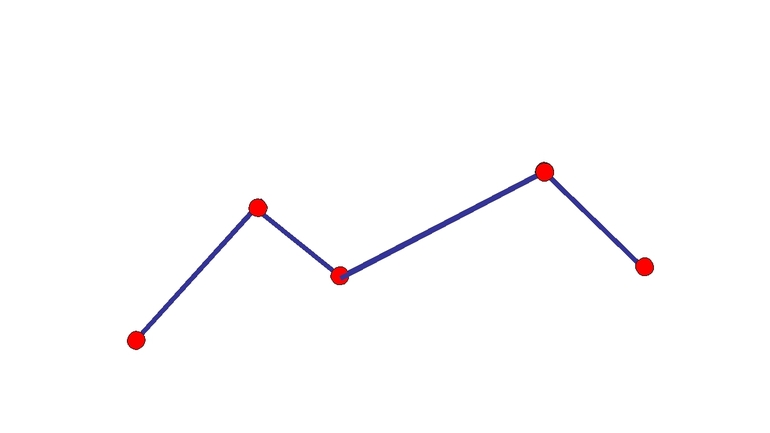
Ломаная

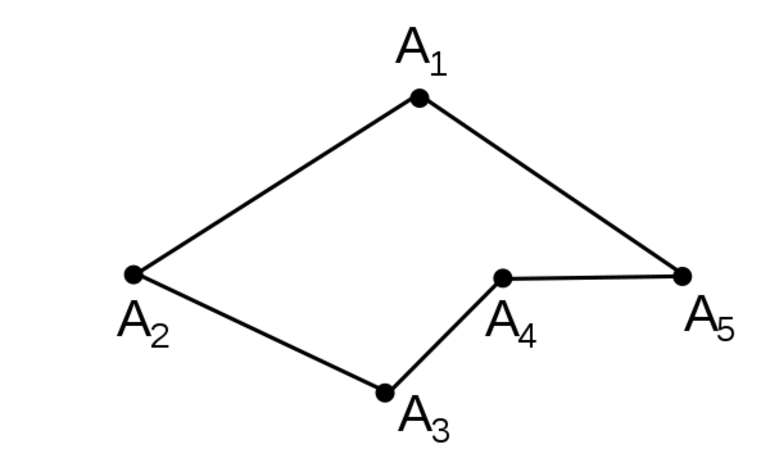
Определение 1. Ломаной (ломаной линией) \( \small A_1A_2. A_A_n \) называется геометрическая фигура, которая состоит из \( \small [ A_1A_2 ],\) \( \small [ A_2A_3 ]. \) \( \small [ A_A_n ]\) последовательно соединенных своими концами отрезков и никакие последовательные две отрезки\( \small [ A_A_ ]\) и \( \small [ A_A_ ]\) при \( \small k=1,2. n-2 \) не лежат на одной прямой.

Можно дать и другое определение ломаной:

Невырожденная ломаная

Ломаная, описанная в определении 1 называется невырожденной ломаной.

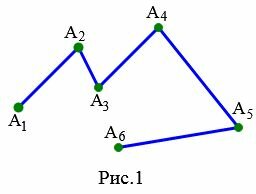
На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.

Вырожденная ломаная

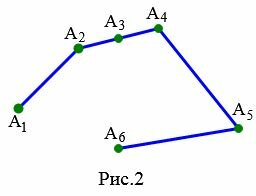На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.

Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.

Звенья ломаной

Звеньями называют отрезки, из которых состоит ломаная.

Вершины ломаной

Конечные точки звеньев ломаной называются вершинами.

На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).

Смежные звенья ломаной

Смежные звенья ломаной − это звенья имеющие общую вершину.

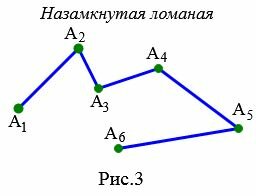
На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).

Смежные вершины ломаной

Смежными вершинами ломаной называют вершины одного звена ломаной.

На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).

Незамкнутая ломанная

Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).

Замкнутая ломанная

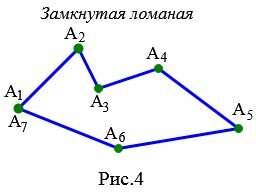На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.

Ломаная с самопересечением

Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.

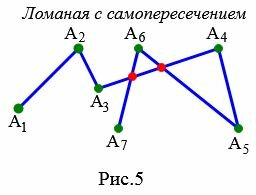Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).

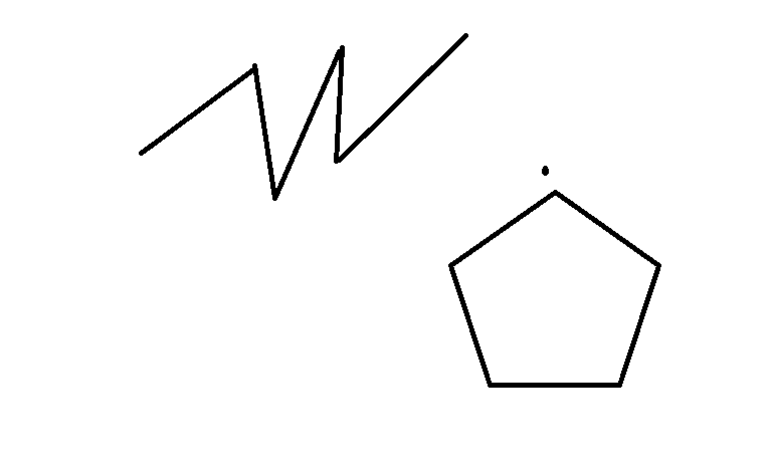
Простая ломаная

Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.

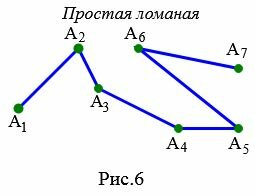Длина ломаной

Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+. +A_A_n, \) где \( \small n \) − количество вершин ломаной.

Теорема. Длина ломаной больше расстояния между первым и последним точками.

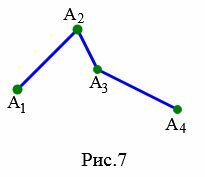Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:

Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:

В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.

В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:

Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.

Аналогично доказывается теорема для ломанной с любым количеством звеньев.

Источник

Краткое описание

Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.

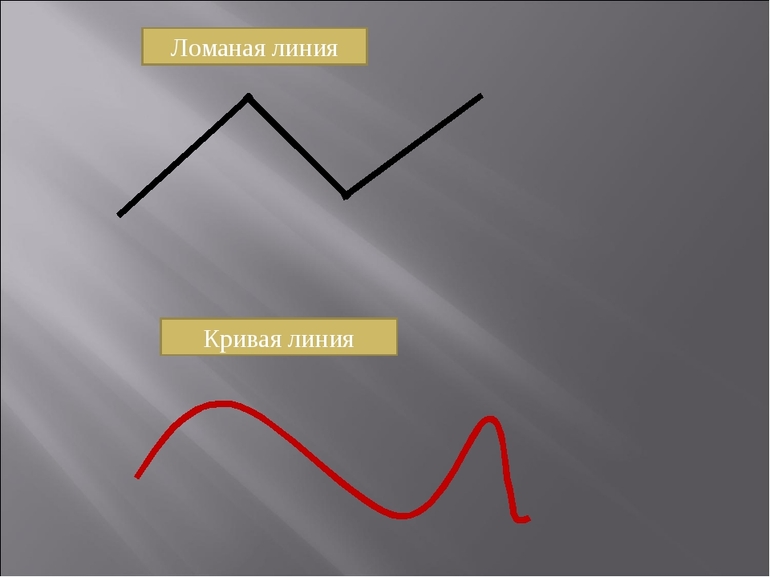
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.

В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.

Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.

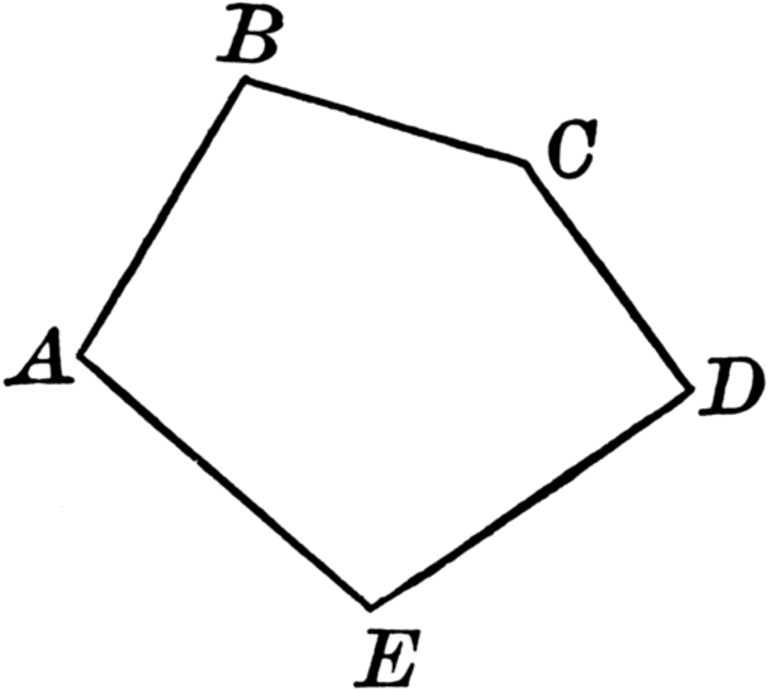
Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.

Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.

Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.

Математическое определение

Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула <1, 2, n — 2>, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.

Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).

Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.

Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:

Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.

Основные разновидности ломаных

Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.

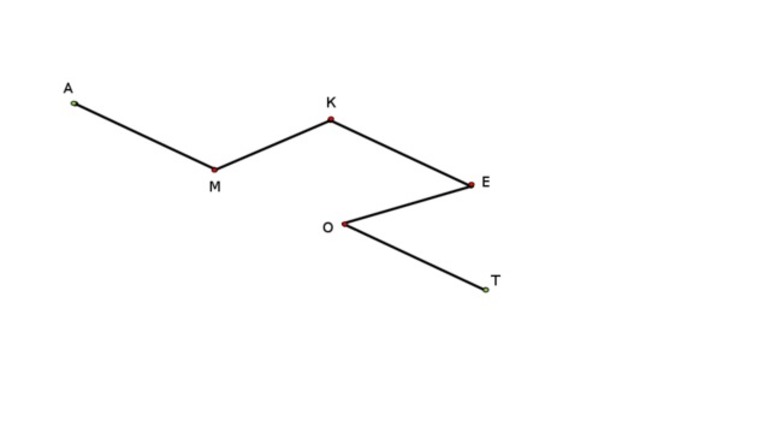
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.

Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.

Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:

Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).

Базовые понятия

Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.

Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.

Особенности построения многоугольников

В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.

Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.

Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.

Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:

Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.

Ключевые нюансы

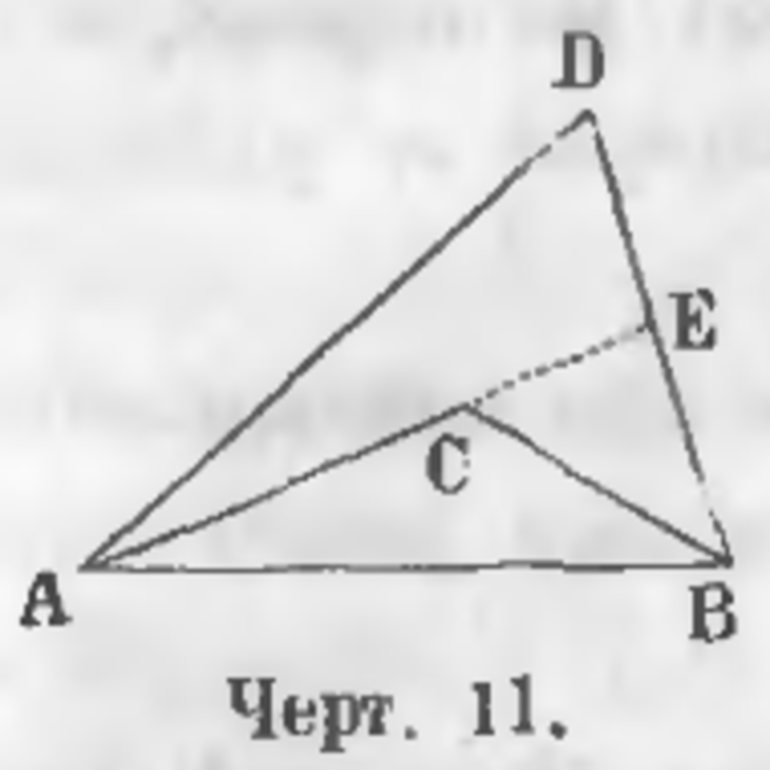
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.

По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.

Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:

Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.

Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.

Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.

Источник

Длина ломаной. Периметр. 2-й класс

Класс: 2

Оборудование: опорные плакаты, компьютерная презентация, карточки заданиями, проволока.

1. Организационный момент

Долгожданный звонок
Начинается урок.

– Ребята, мы сегодня урок проведём в виде путешествия в лес.

Мы в лес за наукой пойдём
Внимание, смекалку с собой возьмём.

Во время путешествия нам предстоит выполнить интересные задания, познакомиться с новым материалом. В конце урока узнаем, какими знаниями мы вернулись.

2. Актуализация знаний

На опушке леса растут деревья,
А на деревьях задания.

– Что у них общего?
– Какое число лишнее?
– В каком порядке расположены числа?
– Какое число самое маленькое?
– Какое число самое большое?
– Установите закономерность и определите следующее число.
– Выразите число 214 в различных единицах счёта.
– Выразите 214 см в различных единицах измерения.

– Расскажите всё, что вы знаете об этих геометрических фигурах.

3. Постановка учебной задачи

– Посмотрите, что у меня в руках? (Проволока)
– Какую геометрическую фигуру она напоминает? (Прямую)
– Посмотрите, что я сделаю этой проволокой (сгибаю в нескольких местах). Можно сказать, что это прямая линия? (Нет)
– Вспомните, как называется такая геометрическая фигура? (Ломаная линия).
– Как называют длину замкнутой ломаной линии? (Периметром)
– Значит, о чём мы будем говорить на уроке? (О длине ломаной, о периметре.)
– Тема нашего урока «Длина ломаной, периметр». Цель урока: научиться находить длину ломаной и периметр.

4. «Открытие» детьми нового знания

Но вот и попали
Мы в сказочный лес
Лес этот полон
Прекрасных чудес.

– Какая эта фигура?
– Назовите признаки ломаной линии. (Ломаная состоит из отрезков, конец одного отрезка является началом другого, 2 соседних отрезка не лежат на одной прямой)
– Отрезки ломаной линии называют звеньями ломаной, место, где соединяются 2 звена, называется вершиной.
– Покажите звенья и вершины ломаной линии. (1 ученик выходит к доске и показывает)

– Какие геометрические фигуры вы видите?
– Какая из ломаных имеет больше всего звеньев?
– Какая – меньше звеньев?
– Какая из ломаных самая длинная? (Ответы детей)
– Как доказать? (Нужно измерить длину ломаной).
– Как измерить длину ломаной? (Измерить длину каждого звена и результаты сложить).
– Ребята, у вас на партах карточки с рисунками ломаных линий. Измерьте длину каждого звена и найдите длину ломаной. Работаем в парах.
– Проверим. Какая длина 1 ломаной линии? 2?
– Какая самая длинная?
– Как вы нашли длину ломаной? Сделаем вывод.
Вывод. Чтобы найти длину ломаной нужно длину её звеньев сложить.
– Значит, что называют длиной ломаной? (Длиной ломаной называют сумму длин её звеньев.)

– Можем ли мы эти линии назвать ломаными? (Да)
– Чем они отличаются от предыдущих? (Это замкнутые ломаные линии).
– Можем найти длины этих ломаных?
– Что нужно для этого сделать? (Измерить длину каждого звена и найти сумму длин всех звеньев ломаной).
– Измерьте длину каждого звена и найдите длину замкнутой ломаной лини. Продолжаем работу в парах.
– Проверим: длина 1 замкнутой линии – …, 2 – ….
– Какие фигуры образуют замкнутые ломаные линии? (Многоугольники)
– Находя длину замкнутой ломаной, вы находили сумму длин всех сторон многоугольника.
– Вспомните, как называют сумму длин сторон многоугольника? (Периметром)
Сумму длин всех сторон многоугольника называют периметром.
– Как найти периметр многоугольника? (Чтобы найти периметр многоугольника нужно длину всех сторон сложить.)

5. Физминутка (под музыку Е. Железнова «Игровая гимнастика».)

Поляна «Отдыхай-ка»

Утром на лесной опушке
Собираются зверюшки.
Все приучены к порядку
Дружно делают зарядку.
1-2-3 …
Привыкайте все к порядку:
Начинайте день с зарядки!

– Почему нужно делать зарядку?

6. Первичное закрепление.

Поляна «Закрепляй-ка»

– Прочитайте задачу.
– Что нужно сделать?
– Как найти длину ломаной?
– Эту задачу вы решите дома. Запишите в дневник.

Поляна «Применяй-ка»

– Где в жизни могут понадобиться знания находить Р? (Когда будем делать рамку для фото, строить забор, прибивать плинтус…)
– А длину ломаной? (Когда будем вычислять путь от дома до школы …)
– Мы с вами решили сделать кормушку, спилили доску-основу длиной 6 дм шириной 4дм. По краям нужно прибить узкую рейку. Какой длины рейка понадобится? (20 см)

– Кормушку мы повесим во дворе Лесной школы. Птицы до нашей кормушки долетят в том случае, если мы поможем « ученикам» Лесной школы.

– Молодцы! Вы помогли и ученикам Лесной школы, и птицам.

– Какую пользу они приносят?
– Поэтому мы должны им помочь?
– В классе мы объявили операцию «Синица». Поднимите руку, кто уже сделал кормушку?

7. Проверочная работа по вариантам

Самопроверка и самооценивание работ.

8. Включение в систему знаний и повторение

1) № 6, с.17 – с объяснением
– Что нужно знать, чтобы дополнить чертёж? (Что здесь целое, что_– часть).
2) № 7, с.17 – самостоятельно. Проверка.
3) № 8, с.17 – «цепочкой»

9. Рефлекция деятельности (итог урока)

– Вот и вышли мы из леса. Какие новые знания мы получили? (Мы научились находить длину ломаной и периметр).
– Как найти длину ломаной? Периметр?
– Чем мы будем заниматься на следующих уроках? (Находить длину стороны многоугольника).

Источник

Ломаная линия

Ломаная линия — это геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами. Ломаной (ломаной линией). называется фигура, которая состоит из отрезков. Точки называются вершинами ломаной, а отрезки звеньями ломаной.

Содержание:

Понятие ломаной

На рисунке 2.39 изображены несколько точек которые последовательно соединены отрезками В результате получилась геометрическая фигура , которая называется ломаной.

Определение. Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков Точки называются вершинами ломаной, а отрезки — звеньями ломаной.

При построении ломаной соседние отрезки не должны лежать на одной прямой. Точки называются соответственно началом и концом ломаной, а составляющие ее отрезки называются звеньями ломаной (рис. 2.39).

Определение. Если концы ломаной совпадают, то ее называют замкнутой.

На рисунках 2.41, 2.42, 2.44 изображены замкнутые ломаные.

Ломаная иногда может пересекать сама себя, т. е. не соседние по порядку звенья ломаной имеют общие точки. В этом случае ломаная называется самопересекающейся или непростой (рис. 2.43, 2.44). Если таких самопересечений нет, то ломаная называется простой. На рис. 2.40, 2.41 изображены простые ломаные.

Длина ломаной

Длина ломаной равна сумме длин ее звеньев.

Можно доказать теорему о длине ломаной.

Теорема 3.

Длина ломаной больше расстояния между ее концами.

Пример:

Звенья ломаной EFMO таковы: EF = 1 см, FM = 4 см, МО = 2 см. Может ли отрезок ЕО равняться: а) 0,5 см; б) 8 см?

Решение:

Из условия задачи имеем:

2. EF = 1 см, FM = 4 см, МО = 2 см. (рис. 2.45)

3. Может ли отрезок ЕО равняться: а) 0,5 см; б) 8 см.

На рис. 2.45 нет отрезка ЕО.

4. Построим отрезок ЕО (построение) (рис. 2.46).

Связь между данной ломаной EFMO и отрезком ЕО определяет теорема о длине ломаной.

5. Длина ломаной EFMO должна быть не меньше длины отрезка ЕО (1, 2, 4, теорема 3).

6. Длина ломаной EFMO равна 7 см (1, 2).

7. Длина отрезка ЕО должна быть не больше 7 см (4, 5).

8. Длина отрезка ЕО может быть равна 0,5 см, но не может быть равна 8 см (1, 2, 7).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник