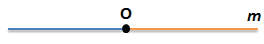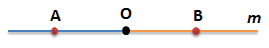Луч что это геометрия
Луч что это геометрия
Построим прямую АВ
(прямая обозначена двумя большими латинскими буквами, например, А и В)
Отметим на прямой АВ точку О
Точка О разбивает прямую АВ на две части (влево от точки О и вправо от точки О)
Части, на которые точка О разбивает прямую АВ, выделены цветом
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча
Назовем получившиеся лучи:
Луч является геометрической фигурой
Луч — это часть прямой, ограниченная с одной стороны
Луч имеет начало, но не имеет конца
Другой способ обозначений
Построим прямую m
(прямая обозначена малой латинской буквой, например, m)
Точка О разбивает прямую m на два луча
Назовем получившиеся лучи
Варианты обозначения лучей
Луч ОВ (обозначение двумя большими латинскими буквами)
Луч ОВ (обозначение двумя большими латинскими буквами)
Луч k (обозначение малой латинской буквой)
Начало луча обозначено буквой О
Луч k (обозначение малой латинской буквой)
Начало луча не обозначено буквой (только отмечено точкой)
Дополнительные лучи
Лучи ОА и ОВ принадлежат одной прямой АВ
Лучи ОА и ОВ имеют общее начало (точка О)
Лучи ОА и ОВ противоположно направлены
При таких условиях лучи ОА и ОВ называются дополнительными
Поделись с друзьями в социальных сетях:
Луч (геометрия)
Более точно, каждая точка O на прямой разбивает множество точек этой прямой, отличных от O, на два непустых подмножества так, что:
Объединение открытого луча с его началом — точкой O — называется лучом с началом в O.
[OA) — обозначение луча с началом O, содержащего точку A.
Для любого расстояния a на заданном луче с началом O существует единственная точка A, находящаяся на расстоянии a от точки O.
Лучами также называют бесконечные промежутки (полупрямые) числовой прямой.
См. также
Полезное
Смотреть что такое «Луч (геометрия)» в других словарях:
НЕЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов… … Энциклопедия Кольера
Риманова геометрия — многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка… … Большая советская энциклопедия
Начертательная геометрия — Начертательная геометрия инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов. Практически, начертательная геометрия ограничивается исследованием объектов … Википедия
Начертательная геометрия* — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Начертательная геометрия — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) перпендикулярами на некоторые две плоскости, которые рассматриваются затем совмещенными одна с другой. При обыкновенном способе изображения предметов линии,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Проекция (геометрия) — У этого термина существуют и другие значения, см. Проекция. Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая… … Википедия
Параллель (геометрия) — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также … Википедия
Алгоритм точки в многоугольнике — Проверка принадлежности данной точки данному многоугольнику На плоскости даны многоугольник и точка. Многоугольник может быть как выпуклым, так и невыпуклым. Требуется решить вопрос о принадлежности точки многоугольнику. Благодаря тому, что… … Википедия
Задача о принадлежности точки многоугольнику — В вычислительной геометрии известна задача об определении принадлежности точки многоугольнику. На плоскости даны многоугольник и точка. Требуется решить вопрос о принадлежности точки многоугольнику. Многоугольник может быть как выпуклым, так и… … Википедия
Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия
Луч что это геометрия
Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой.
Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.
Рассмотрим три луча с общим началом:
Дополнительные лучи
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:
Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.
Обозначение лучей
Луч обозначают одной строчной латинской буквой:
Также луч можно обозначить двумя точками, лежащими на нём:
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC.
Посмотрим на следующий пример:
Луч с началом в точке A можно обозначить как AB или AC.
Луч и угол
Луч — это часть прямой, у которой есть
начало, но нет конца.
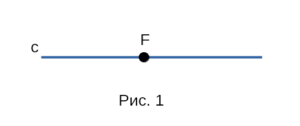
Проведём прямую с и отметим на ней точку F. Точка F разделяет прямую c на две части.
Каждая из этих частей называется лучом, исходящим из точки F. Пример двух лучей,
исходящих из точки F на рисунке 1.
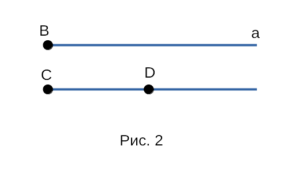
Точка F — начало каждого из лучей. Луч обычно обозначают малой латинской буквой,
либо двумя большими латинскими буквами (первая буква обозначает начало луча,
а вторая буква обозначает какую-нибудь точку на луче). Примеры лучей на рисунке 2.
Угол — геометрическая фигура, состоящая из точки и
двух лучей, исходящих из этой точки.
Лучами называются стороны угла, а точка называется вершиной угла.
Угол обозначают математическим символом ∠.
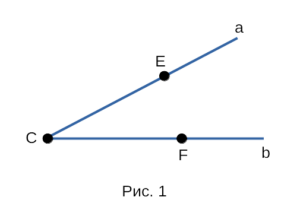
На рисунке 1 изображен угол с вершиной С и сторонами a и b. На сторонах отмечены
точки E и F. Угол в данном случае обозначают вот так: ∠ab, или ∠ECF, или еще проще ∠О.
Если обе стороны угла лежат на одной прямой, то угол развернутый, иначе угол неразвернутый.
На рисунке 2 изображен развернутый угол с вершиной С и сторонами a и b.
Любой угол разделяет плоскость на две части. Существует внешняя
и внутренняя область угла рисунок 3.

Если плоскость разделяет развернутый угол, то каждую из двух частей
можно считать внутренней областью угла. Фигуру также называют углом,
если она состоит из угла и его внутренней области. Если луч исходящий из
вершины неразвернутого угла и проходящий внутри угла, делит угол на два угла.
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Луч – часть прямой, состоящая из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Стороны угла – лучи, из которых состоит угол.
1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Теоретический материал для самостоятельного изучения.
Мы уже познакомились с некоторыми геометрическими понятиями: прямая, точка, отрезок. Сегодня мы рассмотрим ещё два понятия, часто встречающиеся в геометрии – это луч и угол.
Для начала, вспомним, как строятся и обозначаются лучи и углы.
Для этого проведём прямую а, отметим на ней точкуО, которая разделит прямую на две части. Эти части прямой называются лучами, исходящими из точки О. А сама точка О, называется началом каждого из лучей.
Луч принято обозначать как одной малой латинской буквой, например, а.
Или двумя большими латинскими буквами, например, ОА.
При этом стоит помнить, что первая буква всегда обозначает начало луча, а вторая– это любая точка на луче.
Теперь рассмотрим понятие угол.
Начнём с определения.
Угол – это часть плоскости, ограниченная двумя лучами с общим началом.
Лучи – это стороны угла.
В данном случае, это стороны ОА и ОВ.
Общее начало сторон, в данном случае О – это вершина угла.
Углы принято обозначать как двумя малыми латинскими буквами, по названию сторон угла, например, ∠hk,
так и тремя большими латинскими буквами, например, тот же угол можно обозначить ∠АОВ, где вершина угла будет стоять в середине обозначения угла.
Или одной большой латинской буквой, обозначающей вершину угла. Например, тот же угол можно обозначить буквой∠О, по вершине угла.
Далее введём понятия, связанные с углами.
Во-первых, рассмотрим угол, который называют развёрнутым, его обе стороны лежат на одной прямой. Например, ∠С– развёрнутый.
В дальнейшем будем рассматривать углы меньше развёрнутого.
Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Во-вторых, плоскость, на которой изображён любой угол, кроме развёрнутого, делится на две области: внутреннюю и внешнюю.
В развёрнутом углу, любая часть считается внутренней.
На рисунке изображён угол. Какие из точек лежат внутри угла и вне его?
Внутри угла лежат точки: М, Е, К.
Вне угла лежат точки: Р, D, N.
Отметим, что точкиВ и С лежат на сторонах углаО.
Продолжая изучать углы, отметим, что если внутри угла из его вершины провести луч, то он разделит угол на два угла.
Например, луч ОС делит ∠АОВ на два угла – ∠ВОС и ∠АОС.
Итак, сегодня мы повторили некоторые сведения о луче и углах; сформировали представления о внутренней и внешней областях угла, меньше развернутого, познакомились с различными обозначениями луча и угла.
Материал для углубленного изучения
Мы разобрали понятие угол, связанное с планиметрией. Но как отмечалось ранее, у геометрии есть ещё один раздел – стереометрия, который изучается в старших классах. Этот раздел изучает пространственные фигуры, одна из таких фигур–двугранный угол. Дадим ему определение: двугранный угол – пространственнаягеометрическая фигура, образованная двумяполуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями. Двугранный угол имеет стороны (иначе их называют грани), это полуплоскости α и β, и ребро, в данном случае это прямая АВ. Как измерить такие углы и их разновидности, вы узнаете в курсе геометрии 10 класса.
№ 1. Какие из точек лежат на стороне угла?
Посмотрите на рисунок. На нём изображён угол ВОС, соответственно точки B и C лежат на сторонах угла, других точек нет.
№ 2. Сколько углов изображено на рисунке?
Решение. Перечислим все углы, изображённые на рисунке.
СОВ, ВОА, АОD, DОС и развёрнутые углы СОА и DОВ. Получается 8 углов.