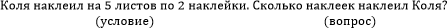Математическая модель задачи что это такое

Что такое математическая модель?

Понятие математической модели.

Например, нам нужно посчитать расходы (Р) на покупки в магазине. Надо купить две булки (Б) и три пачки масла (М). Мы знаем цену булки (ЦБ) и цену масла (ЦМ). Легко можно записать:

Составление (построение) математической модели задачи.

Говоря конкретнее, нужно установить математическую связь между всеми данными задачи.

Но можно выделить три основных момента, на которые нужно обратить внимание.

1. В любой задаче есть текст, как ни странно.) В этом тексте, как правило, имеется явная, открытая информация. Числа, значения и т.п.

3. В любой задаче должно быть дана связь данных между собой. Эта связь может быть дана открытым текстом (что-то равно чему-то), а может быть и скрыта за простыми словами. Но простые и понятные факты частенько упускаются из виду. И модель никак не составляется.

Сразу скажу: чтобы применить эти три момента, задачу приходится читать (и внимательно!) несколько раз. Обычное дело.

Начнём с простой задачки:

Все эти слова нужно превратить в какое-то уравнение. Для этого нужно, повторюсь, установить математическую связь между всеми данными задачи.

С чего начинать? Сначала вытащим из задачи все данные. Начнём по порядочку:

Обращаем внимание на первый момент.

Какая здесь явная математическая информация? 8 рыбин и 20%. Не густо, да нам много и не надо.)

Обращаем внимание на второй момент.

Ищем скрытую информацию. Она здесь есть. Это слова: «20% всех рыбин«. Здесь нужно понимать, что такое проценты и как они считаются. Иначе задача не решается. Это как раз та дополнительная информация, которая должна быть в голове.

Здесь ещё имеется математическая информация, которую совершенно не видно. Это вопрос задачи: «Сколько всего рыбин купил. « Это ведь тоже какое-то число. И без него никакая модель не составится. Поэтому обозначим это число буквой «х». Мы пока не знаем, чему равен икс, но такое обозначение очень нам пригодится. Подробнее, что брать за икс и как с ним обращаться, написано в уроке Как решать задачи по математике? Вот так сразу и запишем:

Возвращаемся к раскрытию информации. Кто не знает, что такое процент, никогда не раскроет, да. А кто знает, тот сразу скажет, что проценты здесь от общего числа рыб даны. А нам это число неизвестно. Ничего не выйдет!

Общее количество рыб (в штуках!) мы не зря буквой «х» обозначили. Посчитать южных рыб в штуках не получится, но записать-то мы сможем? Вот так:

Вот теперь мы скачали всю информацию с задачи. И явную, и скрытую.

Обращаем внимание на третий момент.

Ищем математическую связь между данными задачи. Эта связь настолько проста, что многие её не замечают. Такое часто бывает. Здесь полезно просто записать собранные данные в кучку, да и посмотреть, что к чему.

Вот это уравнение и будет математической моделью нашей задачи.

Прошу заметить, что в этой задаче нас не просят ничего складывать! Это мы сами, из головы, сообразили, что сумма южных и северных рыб даст нам общее количество. Вещь настолько очевидная, что проскакивает мимо внимания. Но без этой очевидности математическую модель не составить. Вот так.

Теперь уже можно применить всю мощь математики для решения этого уравнения). Именно для этого и составлялась математическая модель. Решаем это линейное уравнение и получаем ответ.

Составим математичесскую модель ещё одной задачки:

Спросили Петровича: «А много ли у тебя денег?» Заплакал Петрович и отвечает: «Да всего чуть-чуть. Если я потрачу половину всех денег, да половину остатка, то всего-то один мешок денег у меня и останется. » Сколько денег у Петровича?

Опять работаем по пунктам.

2. Ищем скрытую информацию. Это половинки. Чего? Не очень понятно. Ищем дальше. Есть ещё вопрос задачи: «Сколько денег у Петровича?» Обозначим количество денег буквой «х»:

И вновь читаем задачу. Уже зная, что у Петровича х денег. Вот тут уже и половинки сработают! Записываем:

Остаток будет тоже половина, т.е. 0,5·х. А половину от половины можно записать так:

Теперь вся скрытая информация выявлена и записана.

3. Ищем связь между записанными данными. Здесь можно просто читать страдания Петровича и записывать их математически):

Если я потрачу половину всех денег.

да половину остатка.

Отнимем ещё половину остатка:

то всего-то один мешок денег у меня и останется.

А вот и равенство нашлось! После всех вычитаний один мешок денег остаётся:

Вот она, математическая модель! Это опять линейное уравнение, решаем, получаем:

Задачки, конечно, элементарные. Это специально, чтобы уловить суть составления математической модели. В некоторых задачах может быть гораздо больше данных, в которых легко запутаться. Это часто бывает в т.н. компетентностных задачах. Как вытаскивать математическое содержание из кучи слов и чисел показано на примерах здесь.

В задачах на движение требуется держать в голове формулу-ключ: связь расстояния, скорости и времени. По ссылке можно посмотреть примеры составления модели и решения таких задач.

В задачах на работу надо чётко понимать формулу-ключ: связь времени, производительности труда и объёма работы. Там имеются свои фишки, с которыми можно ознакомиться по ссылке.

Для того, чтобы свободнее ориентироваться в построении математических моделей очень полезно порешать обратные задачи. Т.е. по заданной модели придумать условие задачи. Это, кстати, не так просто.) Тема может быть совершенно любой, фантазия ограничена только математикой. Вот примеры таких заданий:

Составить задачу по математической модели:

х + (х+10) + (х-30) + 20 = 120

Попробуйте придумать задачку, а потом можете найти в уроке Как решать задачи по математике исходную задачу для этой модели. И сравните, для интереса.)

Еще пример, посложнее:

Составить задачу по математической модели:

Исходная задача и её решение приведены в уроке Решение задач на движение. Кстати, по ссылке подробно написано, как эту математическую модель составить.

Составить задачу по математической модели:

1 = 5 · (х + 2х + 2х + 3х + 4х)

Эта задача и её решение расписаны в уроке Задачи на работу.

Ещё одно замечание. В классических школьных задачах (трубы заполняют бассейн, куда-то плывут катера и т.п.) все данные, как правило, подобраны очень тщательно. Там выполняются два правила:
— информации в задаче хватает для её решения,
— лишней информации в задаче не бывает.

В компетентностных и прочих жизненных задачах эти правила строго не соблюдаются. Нету подсказки. Но и такие задачи можно решать. Если, конечно, потренироваться на классических.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

22. Текстовые задачи Читать 0 мин.

22.112. Математическая модель

Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.

Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.

Пример:

Решение любой текстовой задачи можно разделить на несколько основных этапов:

Работа с условием

Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.

Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?

Из рисунка сразу понятен ответ: Петя выше всех.

Пример.

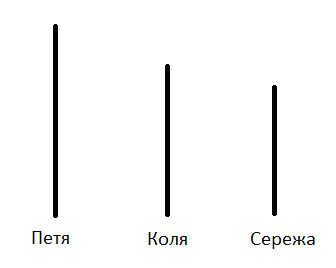
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?

Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.

Составим математическую модель:

Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.

Математическая модель

Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.

y — число мальчиков

Алгебраическая зависимость

Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.

При составлении уравнения особое значение играют используемые предлоги: «в» и «на».

Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?

Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.

Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.

Выразим рост мальчиков.

Петя выше Коли на 20 см: П – 20 = К

Сережа ниже Коли на 10 см: К = С + 10

Подставим в первое уравнение рост Коли: П – 20 = С + 10

Нам нужно найти, на сколько см Петя выше Сережи: П – С

Получаем, что Петя выше Сережи на 30 см.

Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?

Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.

Маша сделала в два раза больше снежинок, чем Коля: К = М/2

Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4

Вместе ребята сделали 12 снежинок: М + К + Р = 12

Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12

Маша сделала 4 снежинки.

Процентная зависимость

С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?

Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.

Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.

Так что же такое один процент?

Процент — это всегда доля какого-то числа.

Чтобы найти 1%, необходимо поделить всё число на 100.

Пример:

Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.

Пример:

Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100

Эту тему мы еще подробно пройдем на курсе.

Рассмотрим несколько примеров работы с процентами в текстовых задачах.

Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов

Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?

Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек

Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?

Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?

На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:

Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880

Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880

Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.

Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.

Источник

Математическая модель

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути, занимаются математическим моделированием: заменяют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект или процесс, построенный на этапе содержательного моделирования. Математическая модель позволяет предсказать поведение реального объекта.

Связанные понятия

Компьютерная модель (англ. computer model), или численная модель (англ. computational model) — компьютерная программа, работающая на отдельном компьютере, суперкомпьютере или множестве взаимодействующих компьютеров (вычислительных узлов), реализующая представление объекта, системы или понятия в форме, отличной от реальной, но приближенной к алгоритмическому описанию, включающей и набор данных, характеризующих свойства системы и динамику их изменения со временем.

Упоминания в литературе

Связанные понятия (продолжение)

В математике решение дифференциального уравнения (или, шире, траектория в фазовом пространстве точки состояния динамической системы) называется устойчивым, если поведение решений, с условиями, близкими к начальным, «не сильно отличается» от поведения исходного решения. Слова «не сильно отличается» при этом можно формализовать по-разному, получая разные формальные определения устойчивости: устойчивость по Ляпунову, асимптотическую устойчивость и т.д. (см. ниже). Обычно рассматривается задача об устойчивости.

К критическим явлениям относятся многочисленные аномалии, наблюдающиеся в фазовых переходах второго рода, например, в точке Кюри в магнетике или в критической точке системы «жидкость-пар». Эти аномалии описываются критическими индексами. В системах появляются очень сильные флуктуации с бесконечным радиусом корреляции. При этом система существенно нелинейна.

Источник

Математическое моделирование при решении задач

Разделы: Математика

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца.
Этот взгляд он должен прививать и своим ученикам».
Д.Пойа.

Обучению решению задач является одной из важнейших составляющих практики преподавания, так как задачи используются не только в качестве основного средства для усвоения математических понятий, но и как материал, способствующий развитию математического мышления и творческой активности учащихся, а также формированию умения применять теоретические знания на практике. Однако, как показывают практика обучения и анализ результатов экзаменационных работ выпускников и абитуриентов, умение решать задачи оставляет желать намного лучшего. И это в особенности касается задач на построение математической модели, вызывающих у учащихся наибольшие затруднения.

Очень часто при решении практической задачи удается, изучив условие задачи, построить её математическую модель, на этой модели осуществить решение задачи, а затем перевести результат решения на язык исходной ситуации, т.е. сделать практический вывод. В этом и состоит

могущество математического метода познания природы, широкая прикладная направленность математики.

В науке широко используется метод моделирования и заключается он в том, что для исследования какого-либо явления или объекта, выбирают или строят другой объект, в каком-то отношении подобный исследуемому объекту. Построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результаты решения этих переносят на первоначальное явление или объект.

Задачи, которые предлагаются в школьных учебниках на моделирование, как правило, приводят лишь к статистическим моделям, в то время как на производстве, транспорте, в сельском хозяйстве и т.п., приходится решать задачи, приводящие к динамичным моделям, т.е. моделям, которые постоянно уточняются, обновляются в зависимости от варьирования параметров моделируемого явления. Рассмотрим на примере решения некоторых задач по теме: » Наибольшее и наименьшее значения функции», каким образом можно формировать у учащихся представление о развитии и уточнении построенной математической модели.

Рассмотрим следующие задачи:

Задача № 1.

Для размещения склада требуется огородить участок прямоугольной формы наибольшей площади имеющейся для этого сеткой длиной 80 м. Найдите длину и ширину участка.

Наиболее часто встречаются два случая:

1) когда склад примыкает к одной стене постройки;

2) одновременно к двум стенам постройки.

Подводя итоги работы над задачей, обращаем внимание учащихся на то, что одна из характерных особенностей математического моделирования состоит в сопоставлении построенной модели с описываемым ей явлением. Результатом такого сопоставления, как правило, является учет каких-то новых моментов в рассматриваемом явлении, следовательно, и уточнение модели.

Задача № 2.

Решение: с помощью производной находим значение скорости v, при которой функция N(v) = 0,001v+ достигает наименьшего значения на интервале (0;+): v=12 км/ч, min N(v) = N(12) 6,728 (рубля на 1км).

Чтобы определить значение коэффициента k, необходимо использовать какие-либо начальные условия. Например, известно, что при скорости в 20 км/ч расходы N(20) = 12,2 рубля на 1 км.

Формулируется задание: «Найдите значение k и определите скорость теплохода по реке против течения, при которой расходы N минимальны».

Наконец, можно нарисовать картину, которая соответствует возвращению теплохода в порт отправления. Тогда возникает задача о нахождении наивыгоднейшей скорости движения по течению. Задание можно сформулировать в таком виде: «Сменив груз, теплоход взял курс в порт отправления. При таком движении расходы снизились на величину, пропорциональную скорости: N (v) = 0001v+ — kv, причем установлено, что при скорости v = 20 км/ч расходы на 1 км пути составляют 5 рублей. Определите k и найдите наивыгоднейшую скорость при движении по течению».

Это задание учащиеся выполняют самостоятельно. В результате получается, что оптимальная при таком движении по реке скорость v 14,1км/ч, а расходы N снижаются до 2,8 рубля на 1км пути.

Далее можно предложить учащимся сравнивать скорости, разным условиям движения теплохода; сравнивать математические модели, описывающие расходы с учетом особенностей течения реки. После выяснения этих вопросов следует отметить, что учет влияния на расходы таких факторов, как скорость ветра, особенности русла реки, швартовки к пристани и т.п., требует более тонкого математического инструментария.

Поэтому можно предложить учащимся упражнение: «Каковы должны быть физические размерности коэффициентов a. b, k, чтобы формула N(v)=аv++ kv правильно описывала расходы на 1км плавания?»

Математическое моделирование некоторых производственных задач опирается на соотношения, известные учащимся, но в ряде случаев оно основывается на зависимостях, которые невозможно установить в рамках школьной программы.

В пищевой, химической и других отраслях промышленности в огромных масштабах используются металлические сосуды, имеющие форму прямоугольного параллелепипеда. По технологическим соображениям эти сосуды изготовляются с заданным отношением высоты k сосуда к одному из размеров основания. В целях экономии требуется, чтобы при изготовлении сосудов заданной ёмкости расход металла, эмалей, лаков, красок, широко применяющихся в качестве покрытий, был возможно меньшим.

Важное практическое значение приобретает такая задача:

Задача № 3.

Каковы должны быть размеры прямоугольного сосуда заданной ёмкости V с заданным значением величины k, чтобы расход металла на его изготовление был наименьшим?

Решение: если расход металла на швы не учитывать, а толщину стенок, дна и крышки считать одинаковой, то за параметр, определяющий расход металла на изготовление сосуда, принять площадь S его поверхности.

Обозначим размеры сосуда через x, y, z и пусть z=ky, то получим:

Функция S имеет наименьшее значение при и что решение задачи задаётся формулами

, , .

Прямоугольные сосуды различной ёмкости производятся в стране в огромных количествах, то становится очевидным, что отступление от оптимальных размеров приводит к значительным убыткам.

Приведем условия задач и дополнительные задания к ним, позволяющие акцентировать внимание на динамическом характере математической модели, выработать первоначальные навыки уточнения модели. Такого рода упражнения могут быть использованы по усмотрению учителя при закреплении умений, связанных с решением задач одномерной оптимизации в домашних, самостоятельных, проверочных и других работах.

Задача № 4.

Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200м, и площадь её при этом оказалась наибольшей. Каковы размеры площадки?

Следующие задачи предлагаются для самостоятельной работы:

Задача № 5.

Стоимость эксплуатации катера плывущего со скоростью V км/ч, составляет N(V)=(90 + 0,4 V ) рублей в час. С какой скоростью должен плыть катер, чтобы стоимость 1км пути была наименьшей?

Задача № 6.

Определить глубину открытого бассейна с квадратным дном и объёмом 500 м так, чтобы на половину его стен и дна пошло наименьшее количество материала.

Дополнительные вопросы: «Как изменится математическая модель, описывающая расход материала на облицовку стен бассейна, если потребуется полностью покрыть стены бассейна материалом?

Каковы оптимальные размеры открытого бассейна?»

Дополнительный вопрос: «Как изменится величина наибольшей кинетической энергии капли, если ее начальная скорость будет отлична от нуля?»

Решение задачи может быть предложено только наиболее подготовленным учащимся.

Задача № 10.

Дополнительные вопросы: «Как изменится математическая модель, описывающая полную стоимость декоративной оградки, если весь участок огородить металлической оградой, цена 1м которой 40 рублей. Каковы оптимальные размеры такого участка?»

Следующую задачу можно рекомендовать учащимся в качестве исследовательской домашней работы в течение некоторого времени.

Задача № 11.

Требуется построить некоторое количество одинаковых жилых домов с общей площадью 40000 м. Затраты на постройку одного дома, имеющего N м жилой площади, складываются из стоимости фундамента, пропорциональной корню квадратному из величины жилой площади дома, и стоимости наземной части, пропорциональной кубу корня квадратного из величины жилой площади. Строительство дома на 1600 м обходится в 184,8 тыс. рублей, причем в этом случае стоимость наземной части составляет 32% стоимости фундамента. Определите, какое количество домов нужно построить, чтобы стоимость затрат была наименьшей, и найдите эту стоимость.

Дополнительное задание может быть связано, например, с учетом применения каких-либо новых материалов для покрытия полов: «Использование более совершенных строительных материалов для отделки покрытий пола уменьшает стоимость дома на величину, пропорциональную площади жилых комнат N. Определите, как в этом случае изменится функция, описывающая расходы на строительство одного дома, если при площади N = 2500 м стоимость дома с улучшенным покрытием пола равна 260 тыс. рублей. Сколько в этом случае нужно построить домов, чтобы сумма затрат была наименьшей? Какова эта сумма?»

Задача 12.

Требуется огородить участок земли, примыкающий одной стороной к морю, с помощью b м проволоки. Какую форму должен иметь участок, чтобы площадь его была наибольшей?

Задача 13.

Литература.

1. А.Г.Цыпкин. «Справочное пособие по методам решения задач по математике».

2. «Алгебра и начала анализа 10-11». Под ред. А.Н.Колмогорова.

3. С.И. Шварцбурд, О.С. Ивашев-Мусатов. «Алгебра и начала анализа.

4. Н.Я.Виленкин, С.И. Шварцбурд. «Алгебра и математический анализ». 10 класс.

Источник