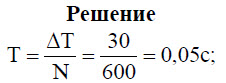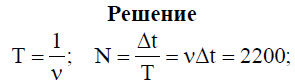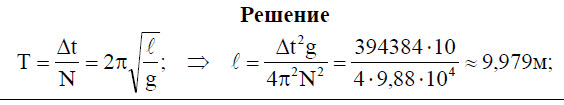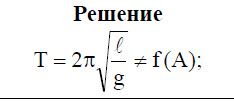Математический маятник совершает колебания по гармоническому закону чему равна амплитуда колебаний
Математический маятник совершает колебания по гармоническому закону чему равна амплитуда колебаний
Маятник совершает вынужденные колебания под действием внешней силы, изменяющейся по гармоническому закону, причём частота изменения этой силы такова, что наблюдается резонанс. Затем частоту изменения внешней силы уменьшают.
Определите, как изменятся через достаточно продолжительное время следующие физические величины: амплитуда колебаний маятника, частота вынужденных колебаний маятника.
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Амплитуда колебаний маятника | Частота вынужденных колебаний маятника |
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты внешней силы с собственной частотой колебательной системы. Другими словами, при резонансе амплитуда колебаний резко возрастает и достигает своего максимального значения. Если мы уменьшим частоту гармонических колебаний внешней силы, то резонанс исчезнет и амплитуда колебаний маятника уменьшится.
Под действием силы, меняющейся с частотой 
груз на пружине совершает вынужденные гармонические колебания с такой же частотой. Следовательно, уменьшение частоты гармонических колебаний внешней силы приведет к уменьшению частоты вынужденных колебаний маятника.
Маятник совершает вынужденные колебания под действием внешней силы, изменяющейся по гармоническому закону, причём частота изменения этой силы такова, что наблюдается резонанс. Затем частоту изменения внешней силы увеличивают.
Определите, как изменятся через достаточно продолжительное время следующие физические величины: амплитуда колебаний маятника, частота вынужденных колебаний маятника.
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Амплитуда колебаний маятника | Частота вынужденных колебаний маятника |
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты внешней силы с собственной частотой колебательной системы. Другими словами, при резонансе амплитуда колебаний резко возрастает и достигает своего максимального значения. Если мы увеличим частоту гармонических колебаний внешней силы, то резонанс исчезнет и амплитуда колебаний маятника уменьшится.
Под действием силы, меняющейся с частотой груз на пружине совершает вынужденные гармонические колебания с такой же частотой. Следовательно, увеличение частоты гармонических колебаний внешней силы приведет к увеличению частоты вынужденных колебаний маятника.
Аналоги к заданию № 10636: 10704 Все
Скорость тела, совершающего гармонические колебания меняется с течением времени в соответствии с уравнением 
где все величины выражены в СИ. Какова амплитуда колебаний скорости? (Ответ дайте в метрах в секунду.)
Общий вид закона изменения скорости тела со временем, совершающего колебания, имеет вид
где 
— амплитуда колебаний скорости. Сравнивая с заключаем, что амплитуда колебаний скорости равна 
А разве закон не имеет вид:
В частном случае, да (если положить 
).
.
Я совсем запутался.
В одних справочниках закон изменения скорости гармонических колебаний выглядит так:
А у вас на сайте увидел совсем другую формулу без «w» после амплитуды.
Как пользоваться такими формулами? Как тогда выглядят законы для координаты и ускорения?
Мой преподаватель говорил, что можна использовать и 1), и 2).
Все довольно просто. Сейчас я, возможно, скажу несколько сложных слов, но затем постараюсь разъяснить их смысл. Для простоты изложения речь будет идти об одномерном случае, на случай многих степеней свободы все легко обобщается.
Это абсолютно общая ситуация. Вспомните, когда мы говорим о движении тела с постоянным ускорением, чтобы в точности задать движение нам нужно именно два числа, начальная координата и начальная скорость.
Тоже самое справедливо и для колебания. Колебание конкретного маятника (то есть маятника с заданной собственной частотой) определяется также двумя числами. Обычно решение уравнения для маятника, получаемого из второго закона Ньютона, записывают в виде 
.
Здесь 
и 
играют как раз роль произвольных постоянных, которые нужно определять из начальных условий. Посчитаем скорость: 
. Пусть нам известно, что в нулевой момент времени координата и скорость маятника были равны 
и 
. Решив систему обычных уравнений 
, можно найти конкретные выражения для и через и .
Не буду приводить ответ в общем случае, если Вы захотите, то легко сделаете это сами. Расскажу только о конкретных случая. Пусть, например, известно, что в нулевой момент времени тело находится в положении равновесия (то есть 
), а его скорость равна своей максимальной величине 
(то есть 
). Тогда получаем для нашего конкретного случая, что система уравнений приобретает вид: 
. Из первого уравнения сразу понятно, что 
(первому уравнению, конечно, удовлетворяет и условие 
, но тогда наше решение получится нулевым, а нас это не устраивает). Второе тогда приобретает вид: 
, откуда 
. Таким образом мы нашли выражения для обеих постоянных. В итоге имеем: 
. При этом для ускорения получается 
. Если теперь 
обозначить через более привычное выражение для амплитуды 
, получатся более привычные формулы.
Рассмотрим еще один пример. Пусть теперь груз находится в крайнем положении, то есть его скорость равна нулю. Будем считать, что от отклонился в отрицательную сторону оси, то есть его координата равна 
. Тогда уравнения на начальные условия приобретают вид: 
. Из второго уравнения 
. Из первого: 
. Таким образом, для координаты имеет: 
(второе равенство при помощи формулы приведения). Для скорости: 
. Для ускорения: 
.
Конкретные формулы зависят от начальных данных. С учетом периодичности синусов и косинусов, пользуясь разными формулами приведения, можно из формул убирать знаки добавлять фазы и т.д.
Что касается формулы в задаче, там нет 
, частоты, так как подставлено ее конкретное значение: 
Гармонические колебания
9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.
Формула периода колебаний
T = t/N
N — количество колебаний [-]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [-]
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
g — ускорение свободного падения [м/с^2]
На планете Земля g = 9,8 м/с2
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
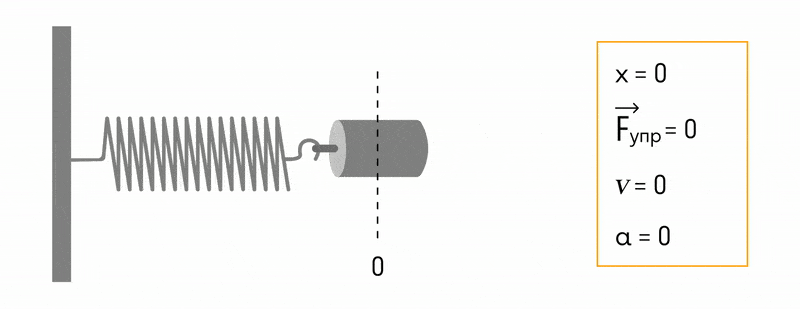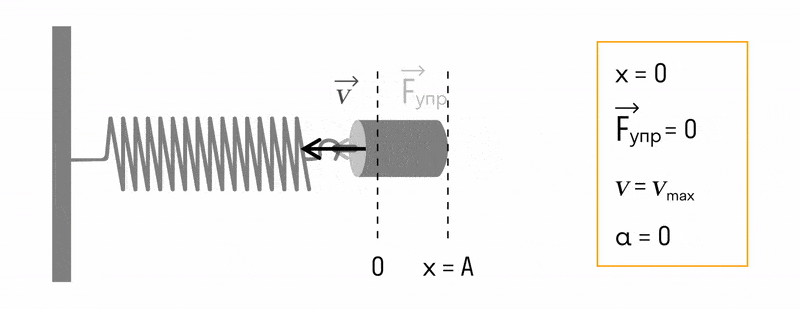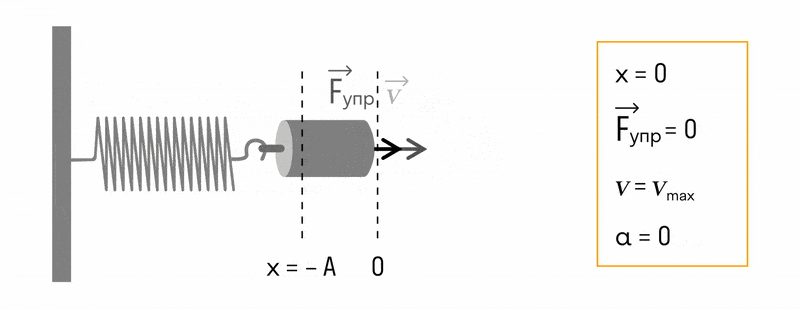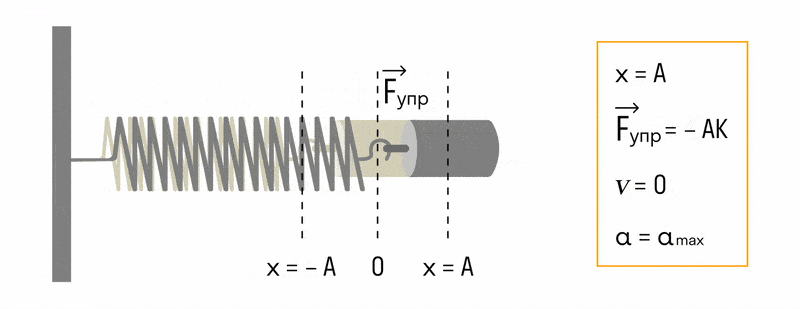
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
маятника
Следовательно, если известны длина и период колебаний маятника, можно определить ускорение свободного падения.
или 
. А так, эта величина бывает разной, она характеризует силу гравитационного поля. В разных точках Земли получаются немного отличающиеся значение (потому что Земля не сферически симметричная). Величина 
зависит даже от того, какие породы залегают под место измерения. На других планетах тоже есть свое ускорение свободного падения, так там оно вообще свое 🙂
