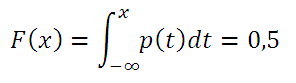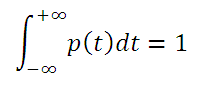Медиана в экселе что показывает
Расчет медианой группы чисел
Предположим, что вы хотите узнать, что такое средний балл в распределении о оценкам учащихся или в образце данных для контроля качества. Чтобы вычислить медиану группы чисел, используйте функцию МЕДИАНА.
Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Снимки экрана в этой статье получены в Excel 2016. Если вы используете другую версию, интерфейс может немного отличаться, но функции будут такими же.
Пример
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Откройте пустую книгу или лист.
Выберите пример ниже.
Примечание: Не выделяйте заголовки строк или столбцов.
Медиана в EXCEL
history 23 октября 2016 г.
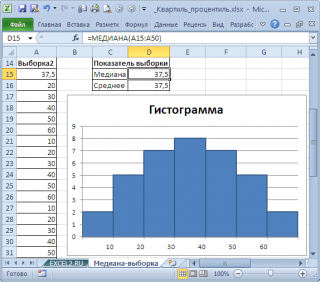
Начнем с медианы для выборок (т.е. для фиксированного набора значений).
Медиана выборки
Для вычисления медианы необходимо сначала отсортировать множество чисел (значения в выборке ). Например, медианой для выборки (2; 3; 3; 4 ; 5; 7; 10) будет 4. Т.к. всего в выборке 7 значений, три из них меньше, чем 4 (т.е. 2; 3; 3), а три значения больше (т.е. 5; 7; 10).
Если множество содержит четное количество чисел, то вычисляется среднее для двух чисел, находящихся в середине множества. Например, медианой для выборки (2; 3; 3 ; 6 ; 7; 10) будет 4,5, т.к. (3+6)/2=4,5.
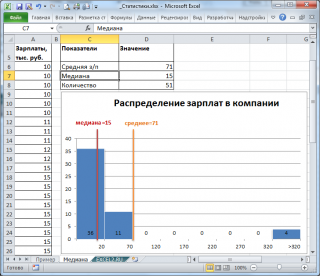
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что как минимум у половины сотрудников зарплата меньше или равна 15 тыс. руб.
Медиана непрерывного распределения
Если Функция распределения F (х) случайной величины х непрерывна, то медиана является решением уравнения F(х) =0,5.
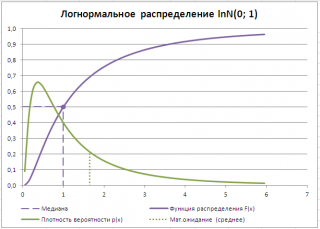
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана вычисляется по формуле =EXP(μ). При μ=0, медиана равна 1.
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице.
Поэтому, линия медианы (х=Медиана) делит площадь под графиком функции плотности вероятности на две равные части.
МЕДИАНА Функция Excel
Медианная функция в Excel
Функция медианы в Excel дает медиану любого заданного набора чисел и относится к категории статистических функций. Медиана любого заданного числа — это число в середине набора. МЕДИАНА измеряет центральную тенденцию, которая является местоположением центра группы чисел в статистическом распределении.
Формула МЕДИАНА в Excel
Ниже приведена формула МЕДИАНА в excel.
Аргументы, используемые для формулы MEDIAN:
число_1, число_2,…, число_n: набор чисел или ссылок на ячейки, обозначающих числовые значения, для которых должна быть вычислена медиана.
Необходимо указать хотя бы один номер. Последующие числа указывать необязательно. В медианной функции можно указать максимум 255 чисел. Входными данными могут быть числа, имена, массивы или ссылки на ячейки, содержащие числа. Любые логические значения и текстовые представления чисел, введенные непосредственно в качестве входных данных, также учитываются функцией Median.
Вывод:
МЕДИАНА вычисляет медиану заданного набора чисел. Ровно половина входных чисел имеет значения больше медианы, а половина чисел имеет значения меньше медианы. Если число входов четное, функция МЕДИАНА вычисляет среднее значение двух чисел в середине. Предположим, что в качестве входных данных задано всего шесть чисел, тогда МЕДИАНА вернет среднее из трех rd и 4 th числа. Функция МЕДИАНА сначала переставляет входные числовые значения в порядке возрастания, а затем определяет среднее значение.
Иллюстрация
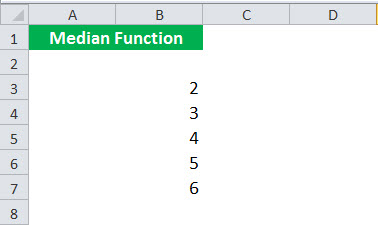
Предположим, вы хотите найти медиану чисел <2, 3, 4, 5, 6>. Эти числа указаны в ячейке B3: B7.
Чтобы вычислить медианную функцию, вы можете использовать следующую формулу MEDIAN:
Формула MEDIAN вернет среднее значение, то есть 4.
Вместо ссылок на ячейки вы можете напрямую указать входные значения как:
Эта формула MEDIAN в Excel вернет тот же результат.
Если вы используете в качестве аргумента четное число значений, например <2, 3, 4, 5, 6, 7>, формула МЕДИАНА выведет среднее из двух средних значений — 4 и 5.
Вывод:
Как использовать функцию МЕДИАНА в Excel?
Функция МЕДИАНА Excel очень проста и удобна в использовании. Давайте разберемся с работой функции МЕДИАНА на некоторых примерах.
Функция «Медиана» в Excel дает меру центральной тенденции или среднего значения и наиболее подходит, когда данные искажены или содержат исключительно высокие или низкие значения. МЕДИАНА — наиболее подходящая мера для данных, классифицированных по порядковой шкале. Функция МЕДИАНА в Excel может использоваться для определения медианы продаж, доходов или расходов.
Пример # 1
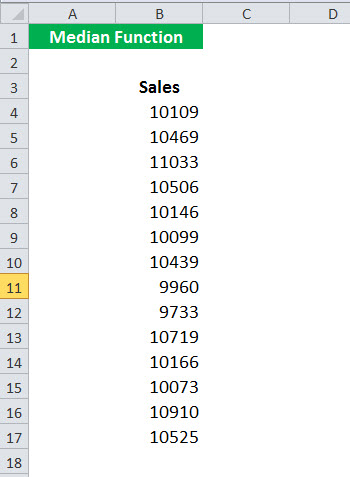
Предположим, у вас есть данные о продажах различных продуктов вашей компании. Данные приведены в ячейке B4: B17.
Теперь вы хотите рассчитать средние продажи. Для этого вы можете использовать формулу MEDIAN в excel:
и нажмите ввод. Он вернет медианное значение.
Пример # 2
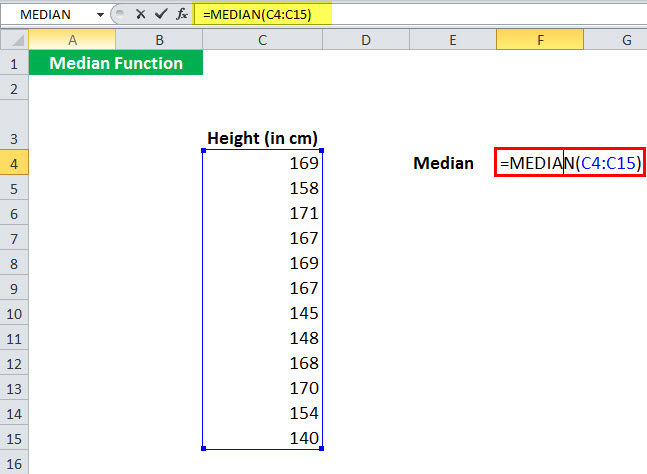
Предположим, в ячейке C4: C15 указан рост 12 учеников. Вы хотите рассчитать средний рост учеников.
Чтобы рассчитать среднюю высоту, вы можете использовать формулу MEDIAN в excel:
Пример # 3
Предположим, у вас есть цены на бензин в разных городах страны за два разных месяца, как показано ниже.
Теперь вы хотите рассчитать средние цены на бензин для каждого месяца, а затем сравнить цены на основе их медианных значений.
Чтобы рассчитать средние цены на август, вы можете использовать формулу MEDIAN в Excel:
и нажмите Enter. Это даст медианное значение для августа, то есть 82,42.
Точно так же вы можете найти медиану для сентября, используя формулу MEDIAN в excel:
Теперь, чтобы узнать, в каком месяце было большее медианное значение, вы можете использовать индекс:
= ИНДЕКС (F4: F5; ПОИСКПОЗ (МАКС (G4: G5); G4: G5; 0))
который вернет Aug.
Пример # 4
Предположим, у вас есть оценки, полученные учащимися класса. В ячейке D4 выставлены оценки: D23.
Теперь вы хотите сравнить оценки с полученными средними оценками. Если полученные оценки выше среднего, учащийся будет считаться выше среднего, в противном случае учащийся будет считаться ниже среднего.
Для этого вы можете использовать следующую формулу МЕДИАНЫ:
и нажмите Enter. Он вернет производительность для 1 ул студент.
Теперь вы можете просто перетащить его к остальным ученикам, чтобы увидеть результаты каждого из учеников.
Давайте подробно рассмотрим формулу MEDIAN в Excel.
Пример # 5
Предположим, у вас есть ежемесячная зарплата отдела вашей компании. Заработная плата указана в ячейке B4: B13.
Теперь вам интересно вычислить центральную тенденцию данной зарплаты. Вы решили, что если стандартное отклонение больше одной трети среднего, вы рассчитаете медиану; в противном случае вы рассчитаете среднее значение.
Для этого вы можете использовать формулу MEDIAN в excel:
= ЕСЛИ (СТАНДОТКЛОН (C4: C13)> (СРЕДНИЙ (C4: C13) / 3), МЕДИАНА (C4: C13); СРЕДНИЙ (C4: C13))
В этом случае стандартное отклонение составляет 29959, а среднее значение — 28300, что ясно показывает, что данные имеют очень высокое стандартное отклонение. Стандартное отклонение в этом случае больше одной трети среднего; таким образом, он сообщит о среднем значении, то есть 15000.
Формулы для расчета среднего по функции МЕДИАНА и МОДА в Excel
Понятие среднее значение за частую подразумевает среднее арифметическое число. То есть результат после разделения суммы чисел на их количество. Так работает функция СРЗНАЧ. Но в программе Excel можно получить еже 2 вида средних значений: МЕДИАНА и МОДА – самое популярное и часто встречаемое значение в списке данных.
Примеры как найти медиальное, популярное и арифметическое среднее
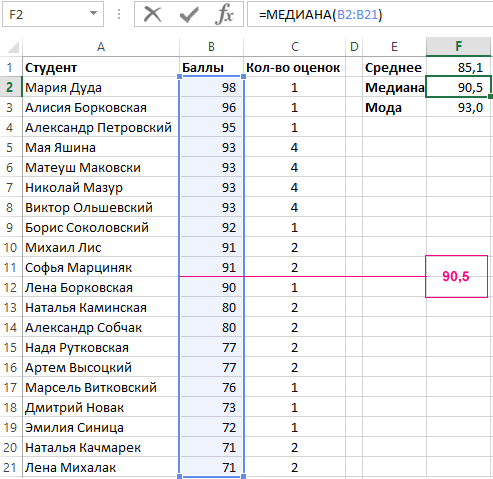
Ниже на рисунке представлен список из 20 студентов с оценками их контрольных работ. Допустим, что мы хотим проанализировать все их оценки по всем трем видам средних значений в Excel:
На основе полученных значений сделаем соответствующие выводы.
Три формулы, используемые для расчетов среднего арифметического, медиального и самого популярного значения в диапазоне исходных данных, которые изображены выше на рисунке:
В результате вычислений формул получаем 3 разных значения средний для одной и той же самой группы чисел.
Как найти среднее значение в Excel с помощью функции СРЗНАЧ
Среднее арифметическое число оценок равно 85,1 медиальное – 90,5 и наиболее часто встречаемая оценка 93 балла. Среднеарифметическое число рассчитано с помощью функции СРЗНАЧ, которая суммирует все значения в указанном диапазоне и делит их сумму на их же количество. Сравнение медианы и наиболее часто встречающегося числа со средним арифметическим позволяет получить дополнительную информацию после такого анализа данных.
Формула вычисления среднего значения в Excel по функции МЕДИАНА
Медиану в Excel вычисляют с помощью функции со соответствующим названием МЕДИАНА. Если все оценки будут отсортированы по возрастанию, функция МЕДИАНА будет возвращать значение, которое находится точно по середине списка данных. Так как общее количество оценок представляет собой парное число, данный список не содержит конкретного числового значения. В такие случаи функция возвращает среднее арифметическое число двух значений находящийся наиболее близко к центру. Как видно на рисунке после сортировки списка по убыванию наиболее близко к центру находятся сразу два числа 90 и 91:
Соответственно функция МЕДИАНА возвращает в итоговом результате своих вычислений число 90,5. Что из этого следует?
Большая разница между средним арифметическим числом и медианой означает, что показатели оценок весьма неравномерные. Например, в данному случае большая разница возникает между наибольшими и наименьшими оценками. Если же среди статистических данных находится одно аномально большое или малое значение, оно может существенно влиять на показатель среднего арифметического числа, но не на медиану!
Формула расчета среднего значения в Excel с функцией МОДА
Наиболее популярное значение находится с помощью функции с соответствующем названием МОДА. Данная функция возвращает оценку, которую получило наибольшее количество студентов. На первом рисунке на против оценок отображается их количество в списке. Как видно оценка в 93 балла появляется 4 раза в одном и том же списке – наиболее чаще других оценок. Если в наборе данных каждое значение появляется такое же количество раз (например, все значения уникальны – значит появляются в списке только 1 раз или же в столбце «Кол-во оценок» все значения одинаковы), тогда функция МОДА возвращает код ошибки недоступных данных #Н/Д! Если больше чем одно значение встречается такое же количество раз (например, если бы 91 балл также встречался 4 раза, как и 93 балла), тогда функция возвращает первый найденный результат.
Функция МОДА.ОДН возвращает массив средних значений в Excel
Начиная с версии 2010-й в Excel были введены две новые функции служащие для поиска наиболее популярных значений МОДА.НСК и МОДА.ОДН. Функция МОДА.НСК работает также, как и обычная МОДА возвращает наиболее часто встречаемое значение, если их есть несколько. А функция МОДА.ОДН возвращает целый одномерный массив значений со всеми популярными значениями.
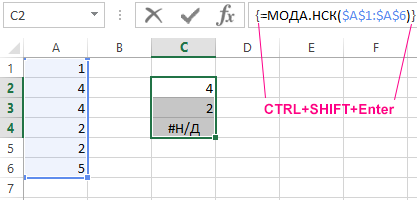
Ниже на рисунке представлен список чисел, в котором есть сращу 2 самых популярных числа (2 и 4). Числа 2 и 4 появляются в общем списке двукратно. Так как функция МОДА.ОДН возвращает целый массив значений, следует для нее соответствующий диапазон ячеей для заполнения этими всеми значениями. На рисунке показано как приготовлены 3 ячейки, несмотря на то, что в данном случае функция МОДА.ОДН возвращает только 2 значения. Если диапазон ячеек больше чем возвращаемый массив с результатами лишние ячейки будут заполнены кодом ошибки недоступных данных #Н/Д!
Формула, которая содержит функцию МОДА.ОДН выполняется в массиве с помощью нажатия комбинации клавиш CTRL+SHIFT+Enter (а не просто Enter как обычно выполняется ввод формул). Если все сделано правильно в строке формул по краям появятся фигурные скобки (<>), которые информируют пользователя о том, что введена формула массива.
Как в Excel посчитать медиану
Чтобы рассчитать медиану в Эксель, можно воспользоваться встроенной функцией МЕДИАНА. Попытаемся разобраться, что такое медиана и рассмотрим методы ее вычисления для выборки или распределения случайных чисел.
Медиана выборки
Итак, медиана представляет собой число, которое выражает середину множества определенного ряда чисел. Таким образом, половина чисел указанного ряда будет больше значения вычисленной медианы, а вторая половина числового ряда – меньше. Для того чтобы определить медиану, нужно отсортировать числовые значения выборки. В итоге медианой выборки цифр 2, 2, 3, 5, 6, 7, 8 будет 5. В данном случае выборка состоит из семи значений – три цифры больше полученной медианы и три – меньше.
Важно! Если выборка состоит четного количества целых цифровых значений, то медиана будет представлена в виде десятичной дроби. Так, медиана выборки ряда 2, 2, 3, 5, 6, 7, 8, 10 составляет 5,5.
Вычисление медианы выборке через возможности Excel осуществляется при помощи соответствующей функции МЕДИАНА. В скобках формулы можно проставить до 255 значений, из которых необходимо вычислить медиану.
Функция МЕДИАНА с выборкой из семи чисел
Медиана не всегда совпадает со средним цифровым значением из представленного ряда. Как правило, совпадение бывает только при симметричном тождестве относительно среднего показателя.
Обратите внимание! Медиана – это не то же самое, что среднее значение. Средний показатель выборки чисел 2, 2, 3, 5, 6, 7, 300 соответствует значению 46,42857, медиана при этом все еще равна 5, так как соотношение чисел больше 5 и меньше не изменилось.
Медиана непрерывного распределения
Теперь рассмотрим расчет медианы в случае непрерывного распределения. Показатель медианы – это результат решения функции распределения случайных непрерывных числовых величин. Если показатель функции распределения (т.е. функция плотности) известен, то значение медианы можно вычислить по такой формуле:
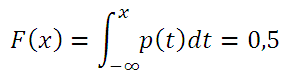
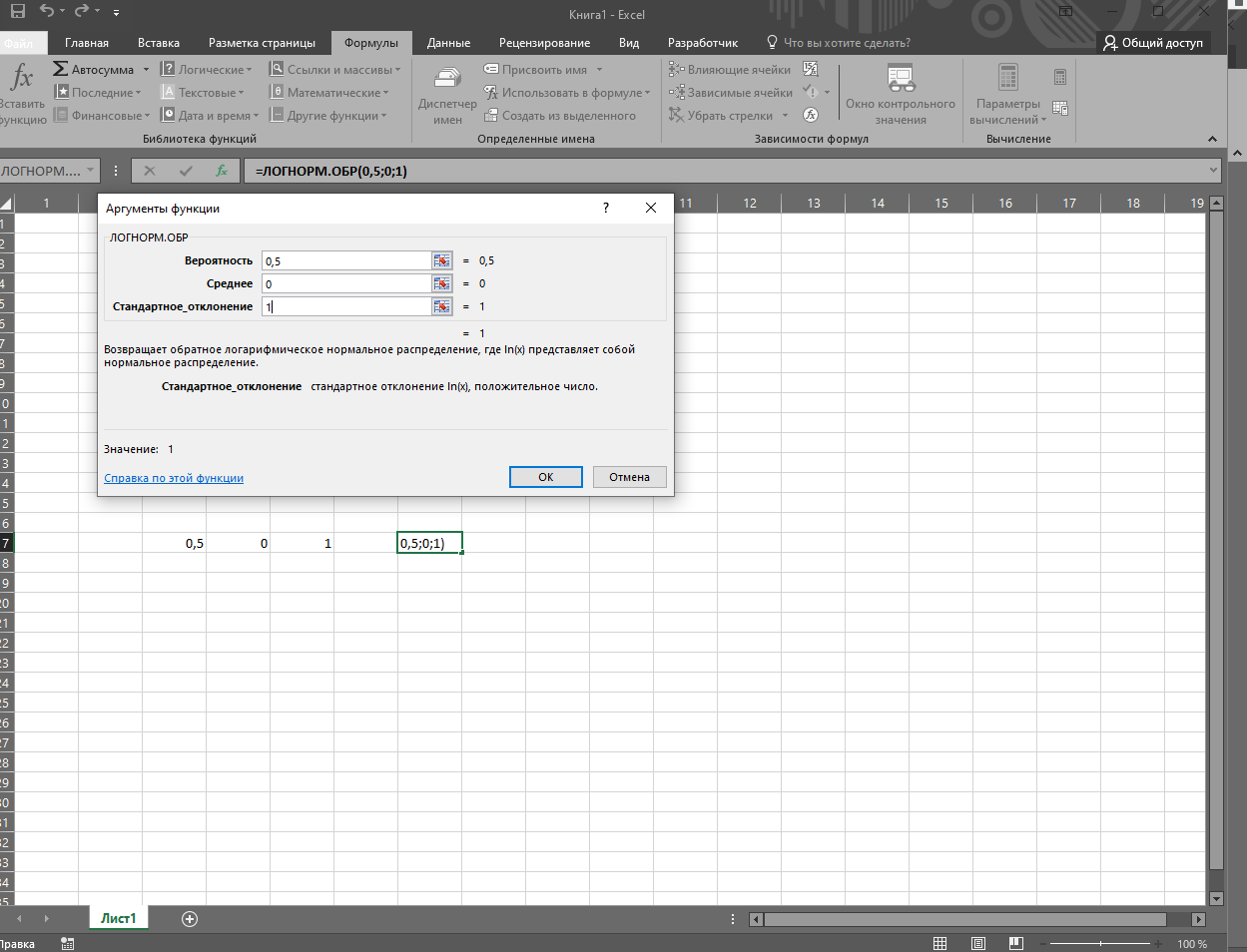
При решении данного уравнения аналитическим методом при логнормальном распределении LnN (µ; σ; 2), значение медианы модно вычислить благодаря формуле =EXP (µ). При условии, что µ=0, медиана будет равна 1. В программе Excel результат медианы для логнормального распределения, представленная формулой LnN (0; 1) вычисляется через функцию =ЛОГНОРМ.ОБР (0,5; 0; 1).
Функция МЕДИАНА
Применяя функцию МЕДИАНА в Эксель, можно вычислить значение середины числового множества. Синтаксическое выражение представляет собой формулу =МЕДИАНА (число 1; [число 2]…). Аргументы «Число 1», «Число 2» и так далее до «Число 255». Первое значение – это обязательное значение, последующие – необязательные, но именно они помогают вычислить медиану.
Следует отметить! В качестве аргументов могут использоваться не только числовые значение, но и ссылки, имена, массивы. Если ссылка или массив частично представлены в виде текста или в выборке есть пустые ячейки, то эти значения не учитываются в процессе вычислений. Использование текстового формата в аргументах приводят к ошибкам в работе функции.
Среднее значение ряда чисел
Рассмотрим вариант расчета средних значений определенного ряда чисел. Например, это может быть средняя температура воздуха в конкретный день года, выполнение поставленных задач сотрудниками и так далее. Для выполнения данного вычисления потребуются три важных параметра:
Указанные параметры при симметричном распределении числового ряда своих значений не меняют, а при асимметричном распределении они могут меняться.
Вычисление значений непрерывного ряда
При определении среднего значения непрерывного числового ряда необходимо осуществить определенный порядок действия:
Среднее взвешенное значение
Здесь случае придется использовать несколько функций – СУММ и СУММПРОИЗВ. Попробуем рассчитать среднюю стоимость единицы товара при наличии трех товаров и количества проведенных продаж. Синтаксис формулы выглядит таким образом: =СУММПРОИЗВ (R[-3]C : R[-3]C[1] : R[-1]C[1]) / СУММ (R[-3]C[1] : R[-1]C[1]). После выполнения данной функции получим среднее значение стоимости одной единицы товара 184,5238095
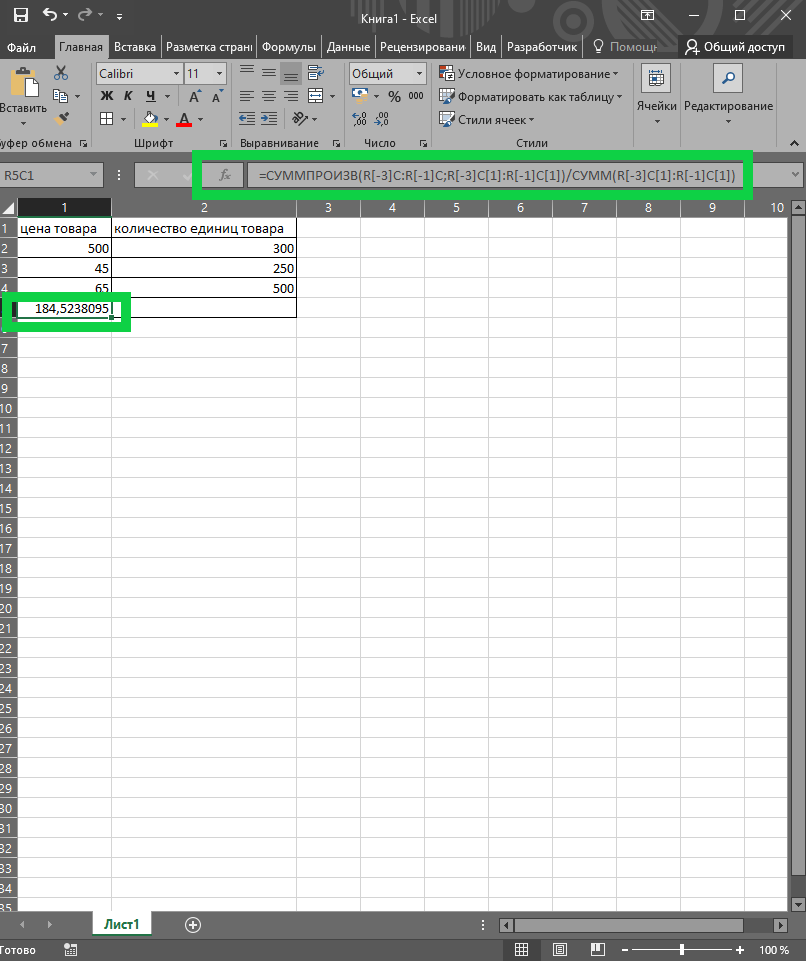
Вычисление без учета нулевых значений
Чтобы в процессе вычислений не учитывались нулевые значения, необходимо воспользоваться двумя функциями – ЕСЛИ и СРЗНАЧ. Рассмотрим пример. В представленном числовом ряду 4, 6, 8, 0, 5, 8 необходимо найти среднее значение, но с условием исключения нулевого значения. Функция будет иметь такой синтаксис: =СРЗНАЧЕСЛИ (А2:А7; “<>0”). В итоге результат функции без нуля будет равен 6,2.
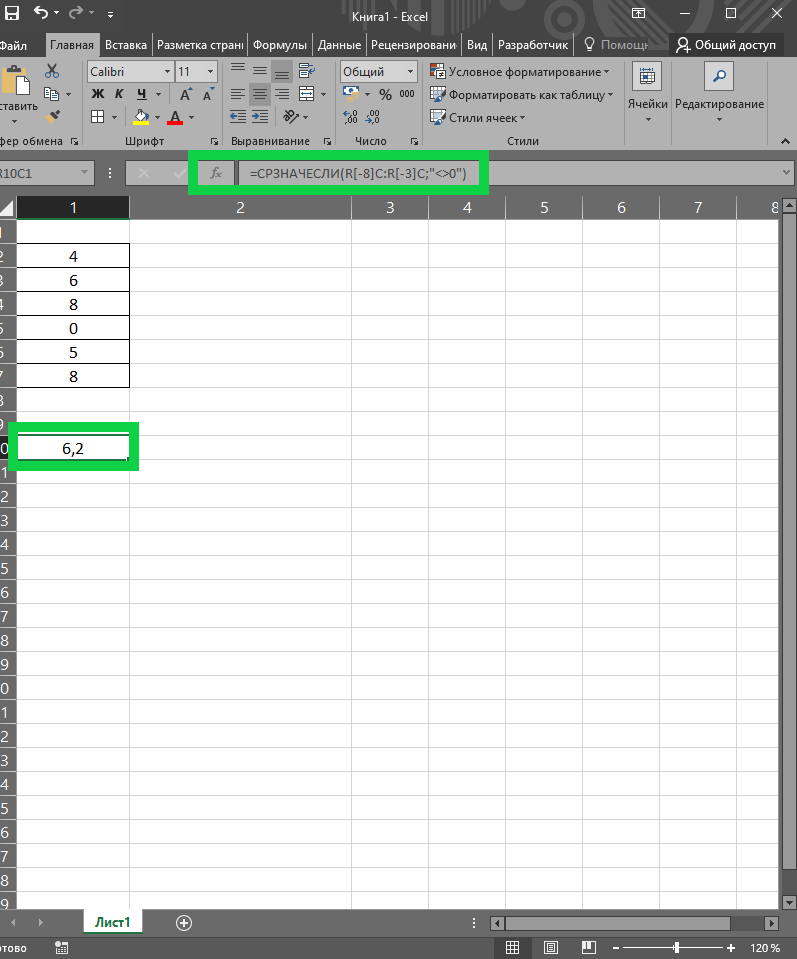
Полезные видео
Ознакомиться с основными принципами вычисления медианы в программе Excel можно, просмотрев несколько обучающих роликов в YouTube