Сонаправленные векторы что это

Вектор. Определение и основные понятия

Обозначение вектора

Направление вектора (от начала к концу) на рисунках отмечается стрелкой.

Длина вектора

Нулевой вектор

Длина нулевого вектора равна нулю.

Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.

Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.

Длина вектора на плоскости

Длина вектора в трехмерном пространстве

Длина вектора в n-мерном пространстве

Коллинеарные вектора

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами

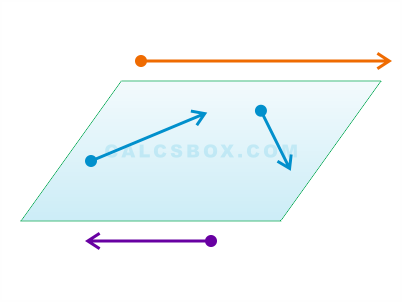
Сонаправленные вектора

Противоположно направленные вектора

Компланарные вектора

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Равные вектора

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

© 2021 Все калькуляторы online

Копирование материалов запрещено

Источник

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Источник

Сонаправленные векторы что это

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник