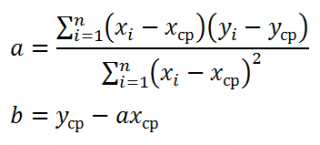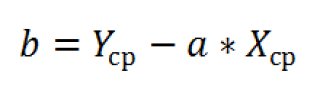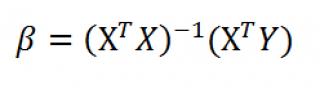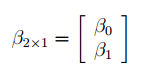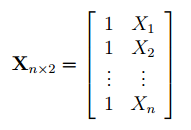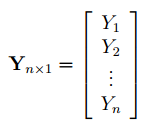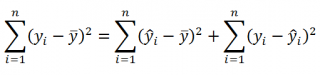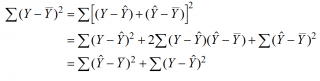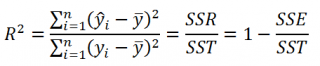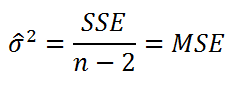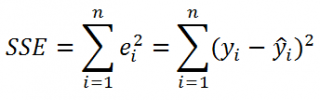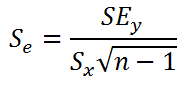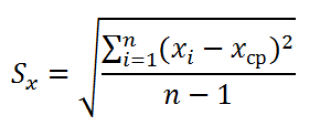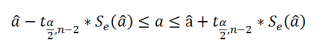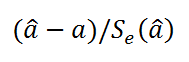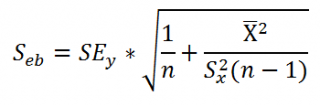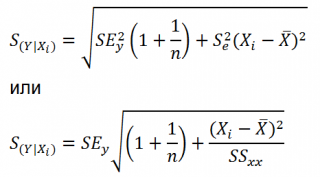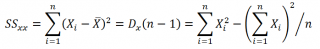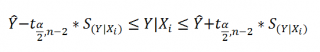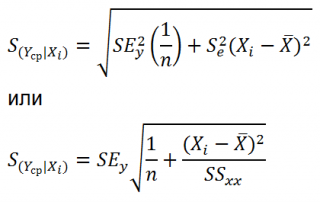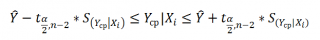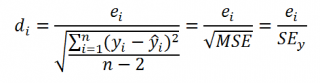t статистика в регрессии excel что значит
Пакет анализа Excel (Регрессия)
Построение линейной регрессии, оценивание ее параметров и их значимости можно выполнить значительнее быстрей при использовании пакета анализа Excel (Регрессия). Рассмотрим интерпретацию полученных результатов в общем случае (k объясняющих переменных) по данным примера 3.5.
| Вывод итогов | |
| Регрессионная статистика | |
| Множественный R | 0,940 |
| R-квадрат | 0,884 |
| Нормированный R – квадрат | 0,868 |
| Стандартная ошибка | 22,87 |
| Наблюдения |
В таблице регрессионной статистики приводятся значения:
Множественный R – коэффициент множественной корреляции 
R—квадрат – коэффициент детерминации R 2 ;
Нормированный R—квадрат – скорректированный R 2 с поправкой на число степеней свободы;
Стандартная ошибка– стандартная ошибка регрессии S;
Наблюдения –число наблюдений n.
| Дисперсионный анализ | ||||
| df | SS | MS | F | Значимость F |
| Регрессия | 28102,2 | 28102,2 | 53,69 | 0,00016 |
| Остаток | 3663,7 | 523,3 | ||
| Итого |
В таблице Дисперсионный анализприведены:
для строки Регрессия df = k;
для строкиОстатокdf = n – k – 1;
для строкиИтогоdf = n – 1.
2. Столбец SS –сумма квадратов отклонений, равная
для строки Регрессия 

для строкиОстаток 
для строкиИтого 
3. Столбец MSдисперсии, определяемые по формуле MS = SS/df:
для строки Регрессия – факторная дисперсия;
для строкиОстаток– остаточная дисперсия.
4. Столбец F – расчетное значение F-критерия, вычисляемое по формуле
5. Столбец Значимость F –значение уровня значимости, соответствующее вычисленной F-статистике.
Значимость F = FРАСП(F-статистика, df(регрессия), df(остаток)).
Если значимость F 2 статистически значим.
| Коэффи-циенты | Стандартная ошибка | t-cта-тистика | P-значение | Нижние 95% | Верхние 95% | |
| Y | 65,92 | 11,74 | 5,61 | 0,00080 | 38,16 | 93,68 |
| X | 0,107 | 0,014 | 7,32 | 0,00016 | 0,0728 | 0,142 |
В этой таблице указаны:
1. Коэффициенты– значения коэффициентов a, b.
2. Стандартная ошибка–стандартные ошибки коэффициентов регрессии Sa, Sb.
3. t-статистика – расчетные значения t-критерия, вычисляемые по формуле:
t-статистика = Коэффициенты / Стандартная ошибка.
4.Р-значение (значимость t)– это значение уровня значимости, соответствующее вычисленной t-статистике.
Р-значение = СТЬЮДРАСП(t-статистика, df(остаток)).
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное y | Остатки e |
| 72,70 | -29,70 | |
| 82,91 | -20,91 | |
| 94,53 | -4,53 | |
| 105,72 | 5,27 | |
| 117,56 | 12,44 | |
| 129,70 | 19,29 | |
| 144,22 | 20,77 | |
| 166,49 | 24,50 | |
| 268,13 | -27,13 |
В таблице ВЫВОД ОСТАТКАуказаны:
в столбце Наблюдение– номер наблюдения;
в столбце Предсказанное y– расчетные значения зависимой переменной;
в столбце Остатки e– разница между наблюдаемыми и расчетными значениями зависимой переменной.
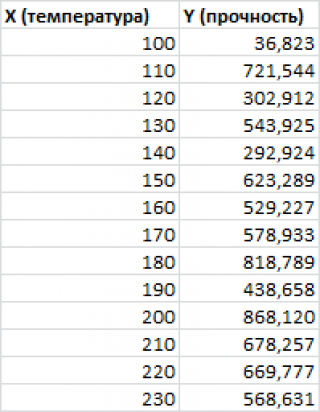
Пример 3.6.Имеются данные (усл. ед.) о расходах на питание y и душевого дохода x для девяти групп семей:
Используя результаты работы пакета анализа Excel (Регрессия), проанализируем зависимость расходов на питание от величины душевого дохода.
Результаты регрессионного анализа принято записывать в виде:
где в скобках указаны стандартные ошибки коэффициентов регрессии.
Коэффициенты регрессии а = 65,92 и b = 0,107. Направление связи между y и xопределяет знак коэффициентарегрессии b = 0,107, т.е. связь является прямой и положительной. Коэффициент b = 0,107 показывает, что при увеличении душевого дохода на 1 усл. ед. расходы на питание увеличиваются на 0,107 усл. ед.
Оценим значимость коэффициентов полученной модели. Значимость коэффициентов (a, b) проверяется по t-тесту:
Р-значение (a) = 0,00080
Величина R 2 = 0,884 означает, что фактором душевого дохода можно объяснить 88,4 % вариации (разброса) расходов на питание.
Значимость R 2 проверяется по F-тесту: значимость F = 0,00016 2 значим при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости.
В случае парной линейной регрессии коэффициент корреляции можно определить как 
T статистика в регрессии excel что значит
В MS Excel экспериментальные данные аппроксимируются линейным уравнением до 16 порядка:
Для получения коэффициентов регрессии используется процедура Регрессия из пакета анализа. Кроме того, могут быть использованы функция ЛИНЕЙН для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ.
Для реализации процедуры Регрессия необходимо:
•выполнить команду Сервис ► Анализ данных;
•в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК;
•в появившемся диалоговом окне задать Входной интервал Y , то есть ввести ссылку на диапазон анализируемых зависимых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку столбца зависимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
•указать Входной интервал X , то есть ввести ссылку на диапазон независимых данных, содержащий до 16 столбцов анализируемых данных. Для этого следует навести указатель мыши на поле ввода Входной интервал X и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю левую ячейку диапазона независимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
•указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;
•если необходимо визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели, следует установить флажок в поле График подбора;
Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y , среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.
Интерпретация результатов. Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:
•переменная Х — а и т. д.
В столбце Р-Значение приводится достоверность отличия соответствующих коэффициентов от нуля. В случаях, когда Р > 0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
Стоит задача предсказания успеваемости абитуриентов по данным вступительных тестов. В качестве исходных данных исследователь имеет для каждого из 10 учащихся предыдущего набора средний балл отметок и 3 показателя тестирования.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Немного теории и основные понятия
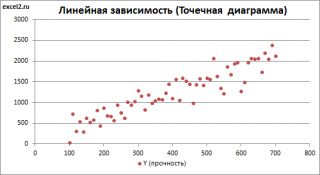
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
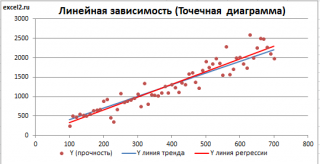
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
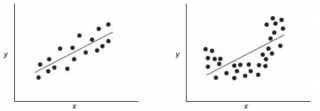
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Подобные рассуждения можно привести для любого значения Хi.
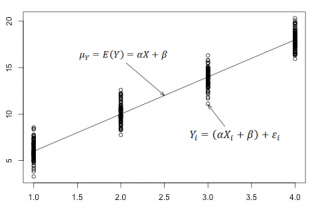
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Задачи регрессионного анализа
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Оценку параметров в MS EXCEL можно выполнить различными способами:
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Чтобы вывести сразу обе оценки:
Оценка неизвестных параметров линейной модели (через статистики выборок)
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
Оценка неизвестных параметров линейной модели (матричная форма)
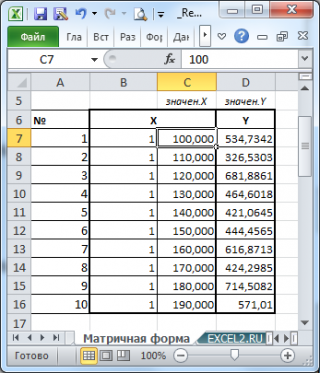
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
В формуле символом Y обозначен столбец значений переменной Y.
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Построение линии регрессии
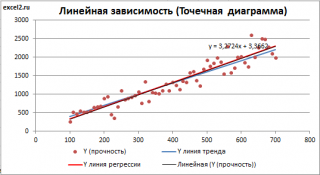
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
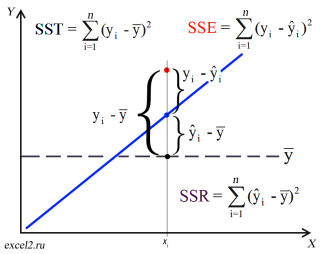
Коэффициент детерминации R 2
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что все три ошибки связаны выражением:
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Для оценки дисперсии σ 2 используют следующую формулу:
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
или с помощью функции ЛИНЕЙН() :
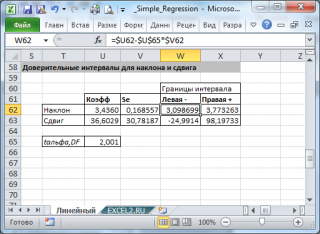
Стандартные ошибки и доверительные интервалы для наклона и сдвига
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
или с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
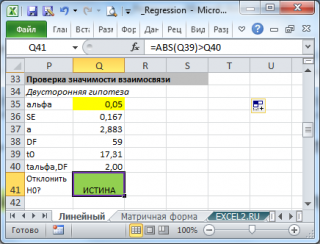
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
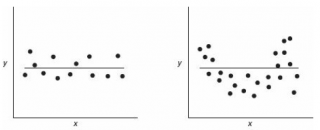
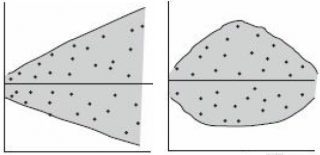
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
Для проверки гипотезы нам потребуется:
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
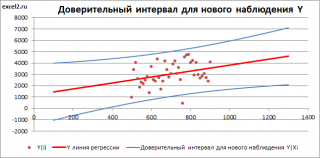
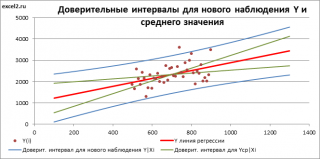
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
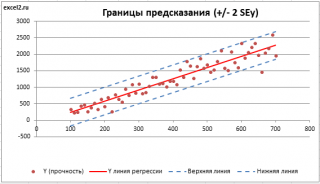
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
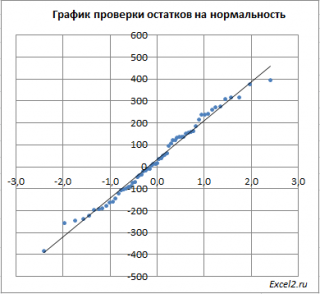
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
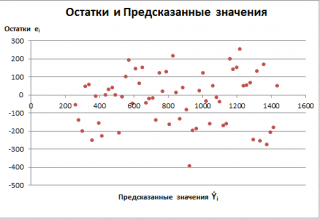
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.