Что такое сонаправленные лучи

Углы с сонаправленными сторонами

Урок 8. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Углы с сонаправленными сторонами»

· введем понятие сонаправленных лучей;

· дадим определение сонаправленных лучей;

· докажем теорему о равенстве углов с сонаправленными сторонами.

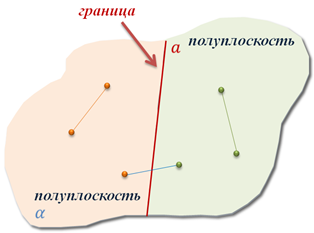
На этом уроке нам понадобится одна из аксиом планиметрии, которая звучит следующим образом: «любая прямая разбивает плоскость на две полуплоскости».

Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.

Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.

Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой.

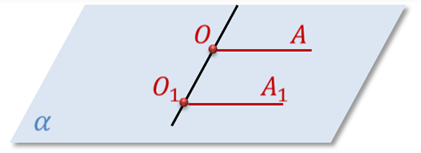
Определение. Два луча ОА и О₁А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО₁.

Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.

Лучи ОА и O₁A₁, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.

Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Доказательство. Рассмотрим случай, когда углы О и О₁ с соответственно сонаправленными сторонами лежат в разных плоскостях.

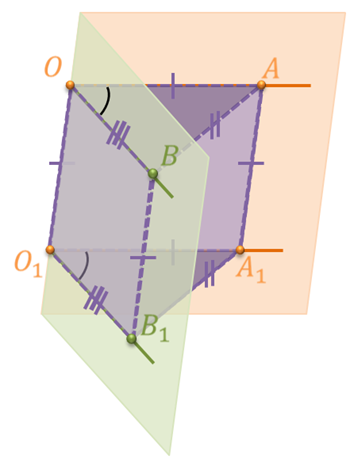
Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОB и

О₁B₁. Т.е. мы имеем два угла АОB и А₁О₁B₁, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А₁О₁B₁.

Отметим на сторонах лучей ОА и O₁A₁ точки А и A₁ так, чтобы отрезки ОА и O₁A₁ были равны. На сторонах лучей ОB и O₁B₁ отметим точки B и B₁ так, чтобы отрезки ОB и O₁B₁ были равны.

Рассмотрим четырехугольник ОАA₁O₁. Так как лучи ОА и O₁A₁ параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА₁О₁ является параллелограммом по признаку параллелограмма. Следовательно, АА₁ параллельно ОО₁ и АА₁ равно ОО₁.

Рассмотрим четырехугольник ОBB₁O₁. Его стороны ОB и O₁B₁ параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB₁O₁ является параллелограммом. Тогда, стороны BB₁ и OO₁ параллельны и равны.

Обратите внимание, мы получили, что прямая AA₁ параллельна прямой OO₁ и прямая BB₁ параллельна прямой OO₁. Тогда по признаку параллельности прямых в пространстве, прямые AA₁ и BB₁ параллельны.

Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA₁ и BB₁ параллельны и равны. А значит, BAA₁B₁ – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A₁B₁ тоже параллельны и равны.

Теперь рассмотрим треугольники АОB и A₁O₁B₁. Стороны ОА и O₁A₁ равны по построению. Стороны ОB и O₁B₁ также равны по построению. Выше мы доказали, что стороны АB и A₁B₁ равны. Значит, треугольники АОB и A₁O₁B₁ равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A₁O₁B₁ равны. Теорема доказана.

Задание. Рассмотрите рисунок и

а) укажите лучи, которые являются сонаправленными;

б) укажите лучи, которые не являются сонаправленными.

Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.

Источник

Определение сонаправленных лучей.

Тема: « Углы и расстояние в пространстве ».

1. Скрещивающиеся прямые. Теоремы о скрещивающихся прямых.

2. Углы с сонаправленными сторонами.

3. Угол между прямыми.

Скрещивающиеся прямые.

Определение. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Две прямые, имеющие лишь одну общую точку, называются пересекающимися.

Итак, возможны три случая взаимного расположения двух прямых в пространстве:

1) прямые пересекаются, т.е. имеют только одну общую точку;

2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;

3) прямые скрещиваются, т.е. не лежат в одной плоскости.

AB⊂α, CD α=C, C ∉ AB

Доказать: AB скрещивается с DC

Доказательство.

Доказательство будем вести методом от противного.

Допустим, АВ и CD лежат в некоторой плоскости β.

Тогда плоскость β проходит через прямую AB и точку C.

Через прямую AB и не лежащую на ней точку C можно провести плоскость, и притом только одну (следствие из аксиом).Следовательно, β≡α.

Но это невозможно, т.к. прямая CD пересекает α. Пришли к противоречию, ⇒ AB и CD лежат в разных плоскостях (скрещиваются). Теорема доказана.

Теорема 2.Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Дано: АВ и CD – скрещивающиеся прямые.

Доказать: ∃ α: AB ⊂α, CD∥α

Доказательство.

2) Проведем плоскость α через пересекающиеся прямые AE и CD.

3) CD ∥ AE, AE ⊂ α ⇒ CD ∥ α.

Любая другая плоскость будет пересекать AB, а значит и параллельную ей прямую CD. Поэтому α – единственная. Теорема доказана

2. Углы с сонаправленными сторонами.

Определение сонаправленных лучей.

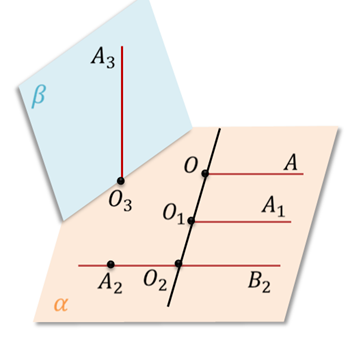
Любая прямая, например ОО₁, рассекает плоскость на две

полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат

в одной полуплоскости, то они называются сонаправленными.

Лучи О₂А₂ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости.

Теорема о равенстве углов с сонаправленными сторонами.Если стороны двух углов соответственно сонаправлены, то такие углы равны.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные

стороны лежат на сонаправленных лучах. Докажем, что эти

На стороне луча ОА и О₁А₁ выберем точки А и А₁так, чтобы отрезки ОА и О₁А₁ были равны. Аналогично, точки В и В₁ выберем так, чтобы отрезки ОВ и О₁В₁ были равны. Рассмотрим четырехугольник А₁О₁ОА. В этом четырехугольнике стороны ОА и О₁А₁ параллельны и равны. По признаку параллелограмма, четырехугольник А₁О₁ОА является параллелограммом. Так как А₁О₁ОА – параллелограмм, то стороны ОО₁ и АА₁ параллельны и равны.

Рассмотрим четырехугольник В₁О₁ОВ. В этом четырехугольнике

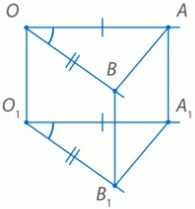
стороны ОВ и О₁В₁ параллельны и равны. По признаку

параллелограмма, четырехугольник В₁О₁ОВ является

параллелограммом. Так как В₁О₁ОВ – параллелограмм, то

стороны ОО1 и ВВ₁ параллельны и равны.

Рассмотрим четырехугольник В₁А₁АВ. В этом четырехугольнике стороны АА₁ и ВВ₁ параллельны и равны. По признаку параллелограмма, четырехугольник В₁А₁АВ является параллелограммом. Так как В₁А₁АВ – параллелограмм, то стороны АВ иА₁В₁ параллельны и равны.

Рассмотрим треугольники АОВ и А₁О₁В₁. Стороны ОА и О₁А₁ равны по построению. Стороны ОВ и О₁В₁ также равны по построению. А как мы доказали, и стороны АВ и А₁В₁ тоже равны. Значит, треугольники АОВ и А₁О₁В₁ равны по трем сторонам. В равных треугольниках против равных сторон лежат равные углы. Значит, углы АОВ и А₁О₁В₁ равны, что и требовалось доказать.

Угол между прямыми.

6.1 Угол между пересекающимися прямыми.

Если прямые пересекающиеся, то мы имеем четыре разных угла.

Углом между двумя прямыми, называется наименьший

из углов между двумя прямыми.

Угол между пересекающимися прямыми а и b обозначим α. Угол α такой, что .

6.2 Угол между скрещивающимися прямыми.

Пусть прямые а и b скрещивающиеся. Выберем произвольную точку О. Через точку О проведем прямую , параллельную прямой а, и прямую , параллельную прямой b. Прямые и пересекаются в точке О. Угол между двумя пересекающимися прямыми и , угол φ, и называется углом между скрещивающимися прямыми.

Решение задач.

Задача 1. Точка D не лежит в плоскости треугольника ABC, точки M, N, и P – середины отрезков DA, DB, и DC соответственно, точка K лежит на отрезке BN. Выясните взаимное расположение прямых:

а) ND и AB; б) PK и BC;

в) MN и AB; г) MP и AC;

д) NK и AC; е) MD и BC.

а) ND ∩ AB = B, поскольку N лежит между B и D;

б) PK пересекается с BC, поскольку PK не является средней линией BCD и поэтому не параллельна BC (PK ∩ BC = P1).

в) MN параллельна AB, т.к. MN – средняя линия ABD. Средняя линия треугольника параллельна основанию (MN AB).

г) MP параллельна AC, т.к. MP – средняя линия ACD (MP AC);

д) NK и AC скрещивающиеся, т.к. они не принадлежат одной плоскости;

е) MD и BC – скрещивающиеся, т.к. не принадлежат одной плоскости.

Задача 2.

Прямая с пересекает прямую а, параллельную прямой b. Докажите, что b и c – скрещивающиеся прямые.

Доказать: с и b – скрещиваются

Доказательство

1. .

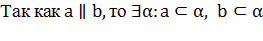
Т.к., по условию задачи, , то через них можно провести плоскость, т.е. существует некоторая плоскость α, содержащая прямые a и b

2.

Прямые a и c пересекаются. Обозначим точку пересечения буквой M. Так как прямые a и b параллельны, то M не принадлежит b.

3. Ч.т.д.

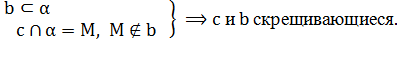
1. Дайте определение скрещивающихся прямых.

2. Дайте определение параллельных прямых.

3. Дайте определение пересекающихся прямых.

4. Какие существуют варианты взаимного расположения двух прямых в пространстве.

5. Сформулируйте теоремы о скрещивающихся прямых.

6. Дайте определение сонаправленных лучей.

7. Сформулируйте теорему о равенстве углов с сонаправленными сторонами.

8. В случае пересекающихся прямых чему равен угол ?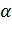

Литература

1. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций : базовый и углубл. уровни / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.].- 3-е изд.- М.: Просвещение, 2016.- 255с.

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с.

Источник

§ 15. Углы

15.1 Сонаправленность лучей

Два луча а и b называются сонаправленными, если они перпендикулярны некоторой плоскости α и лежат с одной стороны от неё (рис. 125).

Для сонаправленных лучей а и b употребляется обозначение: а ↑↑ b.

Основной признак сонаправленности лучей даёт следующая лемма:

Доказательство. Пусть лучи а и b сонаправлены с лучом с. Докажем, что а и b сонаправлены. Так как a ↑↑ с, то они перпендикулярны некоторой плоскости α и лежат с одной стороны от неё. Аналогично b и с перпендикулярны некоторой плоскости β и лежат с одной стороны от β. Так как α и β перпендикулярны одной прямой, на которой лежит луч с, то α || β (рис. 127).

Пусть плоскость α удалена от начала луча с дальше, чем плоскость β. Тогда все лучи а, b, с лежат с одной стороны от плоскости α и все перпендикулярны ей (по теоремам из пп. 8.1 и 8.2.). Поэтому лучи а и b сонаправлены. Если даны луч р и точка А, то из точки А можно провести единственный луч q, сонаправленный с лучом р.

В первом случае один из лучей р или q содержит другой (рис. 128, а). Во втором случае лучи р и q лежат на параллельных прямых с одной стороны от прямой, проходящей через их начала (рис. 128, б).

15.2 Угол между лучами

Угол между сонаправленными лучами полагается равным 0°.

Если лучи р и q не сонаправлены и имеют общее начало, то угол между ними определяется как величина плоского угла со сторонами р и q.

Наконец, в общем случае, когда лучи р и q не сонаправлены и имеют различные начала, поступают так: из любой точки О проводят лучи р’ и q’, сонаправленные соответственно с лучами р и q (рис. 129). Углом между р и q называется величина угла между р’ и q’.

Угол между лучами р и q обозначается так: ∠(pq).

Угол между р и q не зависит от выбора точки О. Это вытекает из следующей леммы:

Доказательство. Пусть даны два угла с вершинами в точках О и О’ и соответственно со-направленными сторонами: р ↑↑ р’ и q ↑↑ q’. В частном случае, когда у этих углов есть стороны, лежащие на одной прямой, утверждение леммы вытекает из равенства соответственных углов при параллельных прямых, пересечённых третьей прямой (рис. 130, а). Поэтому рассмотрим общий случай, когда стороны углов не лежат на одной прямой.

Отложим на сонаправленных сторонах этих углов равные отрезки: ОА = ОА’ на р и р’, а также OВ = O’В’ на q и q’ (рис. 130, б). Проведём отрезки ОО’, АА’, ВВ’, АВ и А’В’. Так как ОА = ОА’ и ОА || ОА’, то четырёхугольник ОАА’О’ — параллелограмм. Поэтому АА’ = ОО’, АА’ || ОО’. Аналогично OO’ = ВВOO’ || ВВ’. Поэтому АА’ = ВВ’, АА || ВВ’, т. е. четырёхугольник АА’В’В — параллелограмм. Следовательно, АВ = А’В’.

Итак, в треугольниках ОАВ и О’А’В’ соответственные стороны равны. Но тогда в них равны и соответственные углы. Итак, ∠AOB = ∠A’O’B’, т. е. ∠(pq) = ∠(p’q’).

Пусть теперь даны два луча р и q. Из точек А и В проведём сонаправленные с ними лучи р, q’ и p», q” (рис. 131). По лемме о сонаправленности лучей (п. 15.1) р’ || р» и q’ || q». А тогда по лемме об углах с сонаправленными сторонами, доказанной в этом пункте, ∠(p’q’) = ∠(p»q»)9 как и говорилось при определении угла между р и q.

15.3 Угол между прямыми

Если прямые пересекаются, то угол между ними, как известно из планиметрии, равен величине вертикальных не тупых углов, образованных этими же прямыми.

Если же прямые скрещиваются, то угол между ними определяют так: через любую точку проводят прямые, параллельные данным, и находят угол между этими прямыми.

В частности, мы можем теперь говорить о взаимно перпендикулярных скрещивающихся прямых и отрезках, если угол между ними равен 90° (отрезки взаимно перпендикулярны, если они лежат на взаимно перпендикулярных прямых).

При таком расширении понятия перпендикулярности прямых, лучей и отрезков остаются справедливыми доказанные ранее теоремы, в которых перпендикулярность рассматривалась лишь для пересекающихся прямых, лучей и отрезков: признак перпендикулярности прямой и плоскости (п. 7.1) и теорема о трёх перпендикулярах (п. 13.2).

В дальнейшем мы будем применять эти теоремы именно в этом более широком смысле. Так, например, прямая а перпендикулярна плоскости α, если она перпендикулярна любым двум пересекающимся прямым, лежащим на этой плоскости. Эти прямые прямую а могут и не пересекать.

15.4 Угол между прямой и плоскостью

Мы уже подробно изучили два важнейших случая взаимного расположения прямой и плоскости: перпендикулярность и параллельность. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости. Поэтому естественно считать, что угол между взаимно перпендикулярными прямой и плоскостью равен 90°. Если же прямая параллельна плоскости или лежит в ней, то угол между ними считается равным 0°.

Рассмотрим общий случай, когда прямая а пересекает плоскость α, но не перпендикулярна ей (рис. 132), т. е. случай прямой, наклонной к плоскости. Характеризуя взаимное расположение таких прямых, часто указывают, насколько прямая отклонилась от перпендикуляра к плоскости. Например, в оптике говорят про угол падения луча света на плоскую поверхность, т. е. про угол между прямой и перпендикуляром (нормалью) к данной плоскости (рис. 132, а). Но в геометрии, оценивая наклон прямой к плоскости, рассматривают не этот угол, а угол, дополняющий его до 90°, т. е. показывающий, насколько прямая отклонилась от плоскости.

Углом между плоскостью и наклонной к ней прямой называется угол φ между этой прямой и её проекцией на данную плоскость (рис. 132, б).

Ясно, почему это определение исключает случай, когда прямая перпендикулярна плоскости: проекцией такой прямой на плоскость будет точка.

Угол между прямой а и плоскостью α обозначается так: ∠aα.

Угол между прямой и плоскостью обладает следующим минимальным свойством: он является наименьшим среди всех углов, образованных данной прямой с прямыми на плоскости. Докажите это свойство сами.

Источник